Keywords: Inverse, LU Factorization, Homogeneous Coordinates, Perspective Projections, Rank
This is the Chapter2 ReadingNotes from book Linear Algebra and its Application.
Matrix Operation
$$
\begin{aligned}
&AB \neq BA
\\
&AB = AC,it’s \space not \space true \space B = C
\\
&AB = 0, it’s \space not \space true \space A = 0 \space or \space B = 0
\\
&(A^T)^T = A
\\
&(A+B)^T = A^T+B^T
\\
&(AB)^T = B^TA^T
\\
&A(BC) = (AB)C
\end{aligned}
$$
- The fastest way to obtain $AB$ on a computer depends on the way in which the computer stores matrices in its memory. The standard high-performance algorithms, such as in LAPACK, calculate $AB$ by columns, as in our definition of the product. (A version of LAPACK written in C++ calculates $AB$ by rows.)
- The definition of $AB$ lends itself well to parallel processing on a computer. The columns of $B$ are assigned individually or in groups to different processors, which independently and hence simultaneously compute the corresponding columns of $AB$.
The Inverse of Matrix
An $n \times n$ matrix $A$ is said to be invertible if there is an $n \times n$ matrix $C$ such that
$$
CA = I \space and \space AC = I
$$
A matrix that is not invertible is sometimes called a singular matrix, and an invertible matrix is called a nonsingular matrix.
一个不可逆的矩阵有时被称为奇异矩阵,一个可逆的矩阵被称为非奇异矩阵
$$
\begin{aligned}
& A = \begin{bmatrix}a & b \\ c & d\end{bmatrix}. \space
if \space ad - bc \neq 0, A \space is\space invertible
\\
& A^{-1} = \frac{1}{ad-bc}\begin{bmatrix}d & -b \\ -c & a\end{bmatrix}
\\
a& d - bc = 0 , A\space is \space not \space invertible
\\
& det A = ad - bc(行列式)
\end{aligned}
$$
If $A$ is an invertible $n \times n$ matrix, then for each $\vec{b}$ in $R^n$, the equation $A\vec{x} = \vec{b}$ has the unique solution $\vec{x} = A^{-1}\vec{b}$.
$$
(A^{-1})^{-1} = A
\\
(AB)^{-1} = B^{-1}A^{-1}
\\
(A^T)^{-1} = (A^{-1})^T
\\
$$
An $n \times n$ matrix $A$ is invertible if and only if $A$ is row equivalent to $I_n$, and in this case, any sequence of elementary row operations that reduces A to $I_n$ also transforms $I_n$ into $A^{-1}$.
💡For example💡:
transform $E_1$ to $I$, get $I$ to $E_1^{-1}$:
$$
E_1 = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ -4 & 0 & 1\end{bmatrix},
E_1^{-1} = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 4 & 0 & 1\end{bmatrix}
$$
An algorithm for Finding $A^{-1}$
Row reduce the augmented matrix $\begin{bmatrix}A & I\end{bmatrix}$. If $A$ is row equivalent to $I$, then $\begin{bmatrix}A & I\end{bmatrix}$ is row equivalent to $\begin{bmatrix}I & A^{-1}\end{bmatrix}$. Other wise, A does not have an inverse.
💡For example💡:
Find the Inverse of the matrix A = $\begin{bmatrix}0 & 1 & 2\\1 & 0 & 3\\4 & -3 & 8\end{bmatrix}$, if it exists.
$$
\begin{bmatrix}A & I\end{bmatrix} =
\begin{bmatrix}0 & 1 & 2 & 1 & 0 & 0\\1 & 0 & 3 & 0 & 1 & 0\\4 & -3 & 8 & 0 & 0 & 1\end{bmatrix}
\sim
\begin{bmatrix}1 & 0 & 0 & \frac{-9}{2} & 7 & \frac{-3}{2}\\0 & 1 & 0 & -2 & 4 & -1\\0 & 0 & 1 & \frac{3}{2} & -2 & \frac{1}{2}\end{bmatrix}
\longrightarrow
A^{-1} = \begin{bmatrix}\frac{-9}{2} & 7 & \frac{-3}{2}\\ -2 & 4 & -1\\ \frac{3}{2} & -2 & \frac{1}{2}\end{bmatrix}
$$
Characterizations of Inversible Matrix
注意,这些性质的应用必须是n $\times$ n的矩阵
Let $A$ be a square $n \times n$ matrix. Then the following statements are equivalent. That is, for a given $A$, the statements are either all true or all false.
a. $A$ is an invertible matrix.
b. $A$ is row equivalent to the $n \times n$ identity matrix.
c. $A$ has $n$ pivot positions.
d. The equation $Ax = 0$ has only the trivial solution.
e. The columns of $A$ form a linearly independent set.
f. The linear transformation $x \rightarrow Ax$ is one-to-one.
g. The equation $Ax = b$ has at least one solution for each $b$ in $R^n$.
h. The columns of $A$ span $R^n$.
i. The linear transformation $x \rightarrow Ax$ maps $R^n$ onto $R^n$.
j. There is an $n \times n$ matrix $C$ such that $CA = I$.
k. There is an $n \times n$ matrix $D$ such that $AD = I$.
l. $A^T$ is an invertible matrix.
Invertible Linear Transformations
Let $T :R^n\rightarrow R^n$ be a linear transformation and let $A$ be the standard matrix for $T$. Then $T$ is invertible if and only if $A$ is an invertible matrix. In that case, the linear transformation $S$ given by $S(x) = A^{-1}x $ is the unique function satisfying equations (1) and (2)
$$
S(T(x)) = x, x \in R^n\tag{1}
$$
$$
T(S(x)) = x, x \in R^n\tag{2}
$$
由于计算机的精度问题,you might occasionally encounter a “nearly singular” or illconditioned matrix—an invertible matrix, that can become singular if some of its entries are changed ever so slightly.
In this case, row reduction may produce fewer than $n$ pivot positions, as a result of roundoff error.
Also, roundoff error can sometimes make a singular matrix appear to be invertible.
Partitioned Matrices
$$
A =
\left[
\begin{array}{ccc|cc|c}
3 & 0 & -1 & 5 & 9 & -2 \\
-5 & 2 & 4 & 0 & -3 & 1 \\
\hline
-8 & -6 & 3 & 1 & 7 & -4
\end{array}
\right]
$$
can also be written as the $2 \times 3$ partitioned (or block) matrix
$$
A = \begin{bmatrix}A_{11} & A_{12} & A_{13} \\
A_{21} & A_{22} & A_{23}\end{bmatrix}
$$
Multiplication of Partitioned Matrices
$$
A : m \times n, B : n \times p
\\
AB = \begin{bmatrix}col_1(A) & col_2(A) & \cdots & col_n(A)\end{bmatrix}
\begin{bmatrix}row_1(B) \\ row_1(B) \\ \cdots \\ row_n(B)\end{bmatrix}\tag{1}
$$
Inverse of Partitioned Matrices
$$
assume\space A_{11}: p\times p, A_{22}: q\times q, A \space invertible.
A = \begin{bmatrix}A_{11} & A_{12}\\
0 & A_{22}\end{bmatrix}\tag{bolck upper triangular}
$$
$$
求逆过程如下:
\\
A_{11}B_{11} + A_{12}B_{21} = I_p\tag{1}
$$
$$
A_{11}B_{12} + A_{12}B_{22} = 0\tag{2}
$$
$$
A_{22}B_{21} = 0\tag{3}
$$
$$
A_{22}B_{22} = I_{q}\tag{4}
$$
$$
(1)(2)(3)(4)\rightarrow
A^{-1} = \begin{bmatrix}A_{11} & A_{12}\\
0 & A_{22}\end{bmatrix} ^ {-1}
=\begin{bmatrix}A_{11}^{-1} &-A_{11}^{-1}A_{12}A_{22}^{-1}\\
0 & A_{22}^{-1}\end{bmatrix}
$$
分块矩阵提高计算机计算效率 When matrices are too large to fit in a computer’s high-speed memory, partitioning permits the computer to work with only two or three submatrices at a time.
Matrix Factorizations 矩阵分解
The LU Factorization
Asume that $A$ is an $m \times n$ matrix that can be row reduced to echelon form, without row interchanges. Then $A$ can be written in the form $A = LU$ , where $L$ is an $m \times m$ lower triangular matrix with $1’s$ on the diagonal and $U$ is an $m \times n$ echelon form of $A$.
The matrix $L$ is invertible and is called a unit lower triangular matrix. 单位下三角矩阵
$$
A = \begin{bmatrix} 1 & 0 & 0 & 0\\ * & 1 & 0 & 0\\ * & * & 1 & 0\\ * & * & * & 1\end{bmatrix}
\begin{bmatrix}
\blacksquare & * & * & * & *\\
0 & \blacksquare & * & * & *\\
0 & 0 & 0 & \blacksquare & *\\
0 & 0 & 0 & 0 & 0
\end{bmatrix}
$$
思考,这样分解有什么好处?
$$
A\vec{x} = \vec{b}
\longrightarrow
L(U\vec{x}) = \vec{b},
\\
let\space \vec{y} = U\vec{x}
\Rightarrow
\\
\begin{cases}
L\vec{y} = \vec{b}\\
U\vec{x} = \vec{y}\tag{2}
\end{cases}
$$
分解后好求解,因为LU都是三角矩阵
💡For example💡:
$$
A =
\begin{bmatrix}
3 & -7 & -2 & 2\\
-3 & 5 & 1 & 0\\
6 & -4 & 0 & -5\\
-9 & 5 & -5 & 12
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 & 0\\
-1 & 1 & 0 & 0\\
2 & -5 & 1 & 0\\
-3 & 8 & 3 & 1
\end{bmatrix}
\begin{bmatrix}
3 & -7 & -2 & 2\\
0 & -2 & -1 & 2\\
0 & 0 & -1 & 1\\
0 & 0 & 0 & -1
\end{bmatrix}
= LU
,
Solve A\vec{x} = \vec{b}, where\space
b =
\begin{bmatrix}
-9 \\5 \\7 \\11
\end{bmatrix}
$$
Solution:
$$
\begin{bmatrix}L & \vec{b}\end{bmatrix} =
\begin{bmatrix}
1 & 0 & 0 & 0 & -9\\
-1 & 1 & 0 & 0 & 5\\
2 & -5 & 1 & 0 & 7\\
-3 & 8 & 3 & 1 & 11
\end{bmatrix}
\sim
\begin{bmatrix}
1 & 0 & 0 & 0 & -9\\
0 & 1 & 0 & 0 & -4\\
0 & 0 & 1 & 0 & 5\\
0 & 0 & 0 & 1 & 1
\end{bmatrix} =
\begin{bmatrix}I & \vec{y}\end{bmatrix}
\\
\begin{bmatrix}U & \vec{y}\end{bmatrix} =
\begin{bmatrix}
3 & -7 & -2 & 2 & -9\\
0 & -2 & -1 & 2 & -4\\
0 & 0 & -1 & 1 & 5\\
0 & 0 & 0 & -1 & 1
\end{bmatrix}
\sim
\begin{bmatrix}
1 & 0 & 0 & 0 & 3\\
0 & 1 & 0 & 0 & 4\\
0 & 0 & 1 & 0 & -6\\
0 & 0 & 0 & 1 & -1
\end{bmatrix} =
\begin{bmatrix}I & \vec{x}\end{bmatrix}
$$
The LU Factorization Algorithm
Suppose $A$ can be reduced to an echelon form $U$ using only row replacements that add a multiple of one row to another row below it. In this case, there exist unit lower triangular elementary matrices $E_1,\cdots,E_p$ such that:
$$
E_p\cdots E_1A = U\tag{3}
$$
Then
$$
A = (E_p\cdots E_1)^{-1}U = LU
$$
where
$$
L = (E_p\cdots E_1)^{-1}\tag{4}
$$
从推导过程可以看出,$A$经历了哪些初等行变换,$L$也同时经历,最终$A$变成了$U$,$L$变成了$I$
It can be shown that products and inverses of unit lower triangular matrices are also unit lower triangular.Thus $L$ is unit lower triangular.
💡For example💡:
Find the $LU$ factorization of $A$.
$$
A =
\begin{bmatrix}
2 & 4 & -1 & 5 & -2\\
-4 & -5 & 3 & -8 & 1\\
2 & -5 & -4 & 1 & 8\\
-6 & 0 & 7 & -3 & 1
\end{bmatrix}
$$
Solution:
$$
A = \begin{bmatrix}
\bbox[border:2px solid red]{2} & 4 & -1 & 5 & -2\\
\bbox[border:2px solid red]{-4} & -5 & 3 & -8 & 1\\
\bbox[border:2px solid red]2 & -5 & -4 & 1 & 8\\
\bbox[border:2px solid red]{-6} & 0 & 7 & -3 & 1
\end{bmatrix}
\sim
\begin{bmatrix}
2 & 4 & -1 & 5 & -2\\
0 & \bbox[border:2px solid red]3 & 1 & 2 & -3\\
0 & \bbox[border:2px solid red]{-9} & -3 & -4 & 10\\
0 & \bbox[border:2px solid red]{12} & 4 & 12 & -5
\end{bmatrix}
\sim
\begin{bmatrix}
2 & 4 & -1 & 5 & -2\\
0 & 3 & 1 & 2 & -3\\
0 & 0 & 0 & \bbox[border:2px solid red]2 & 1\\
0 & 0 & 0 & \bbox[border:2px solid red]4 & 7
\end{bmatrix}
\sim
\begin{bmatrix}
2 & 4 & -1 & 5 & -2\\
0 & 3 & 1 & 2 & -3\\
0 & 0 & 0 & 2 & 1\\
0 & 0 & 0 & 0 &\bbox[border:2px solid red]5
\end{bmatrix} = U
$$
$$
\begin{bmatrix}
2\\-4\\2\\6
\end{bmatrix}
\begin{bmatrix}
\\3\\-9\\12
\end{bmatrix}
\begin{bmatrix}
\\\\2\\4
\end{bmatrix}
\begin{bmatrix}
\\\\\\5
\end{bmatrix}
\\
\div 2
\downarrow
\div 3
\downarrow
\div 2
\downarrow
\div 5
\downarrow
\\
\begin{bmatrix}
1 & & & \\
-2 & 1 & & \\
1 & -3 & 1 & \\
3 & 4 & 2 & 1
\end{bmatrix} = L
$$
👉More About QR Factorization >>
The Leontief Input–Output Model(Omit)
Applications to Computer Graphics
Homogeneous Coordinates
The mathematics of computer graphics is intimately connected with matrix multiplication. Unfortunately, translating an object on a screen does not correspond directly to matrix multiplication because translation is not a linear transformation. The standard way to avoid this difficulty is to introduce what are called homogeneous coordinates.
$$
translation : (x,y)\mapsto(x + h, y + k)\\
homogeneous-translation: (x,y,1)\mapsto(x + h, y + k, 1)
\\
matrix-multiplication:
\begin{bmatrix}
1 & 0 & h\\
0 & 1 & k\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\y\\1
\end{bmatrix}=
\begin{bmatrix}
x + h\\y+k\\1
\end{bmatrix}
$$
Any linear transformation on $R^2$ is represented with respect to homogeneous coordinates by a partitioned matrix of the form $\begin{bmatrix}A & 0 \\ 0 & 1\end{bmatrix}$, where $A$ is a $2 \times 2$ matrix. Typical examples are:
$$
\begin{bmatrix}
\cos\psi & -\sin\psi & 0\\
\sin\psi & \cos\psi & 0\\
0 & 0 & 1
\end{bmatrix},
\begin{bmatrix}
0 & 1 & 0\\
1 & 0 & 0\\
0 & 0 & 1
\end{bmatrix},
\begin{bmatrix}
s & 0 & 0\\
0 & t & 0\\
0 & 0 & 1
\end{bmatrix}
$$
Homogeneous 3D Coordinates
$(x,y,z,1)$ are homogeneous coordinates for the point $(x,y,z)$ in $R^3$. In general, $(X,Y,Z,H)$ are homogeneous coordinates for $(x,y,z)$ if $H \neq 0$
$$
x = \frac{X}{H}, y = \frac{Y}{H}, z = \frac{Z}{H}
$$
💡For example💡:
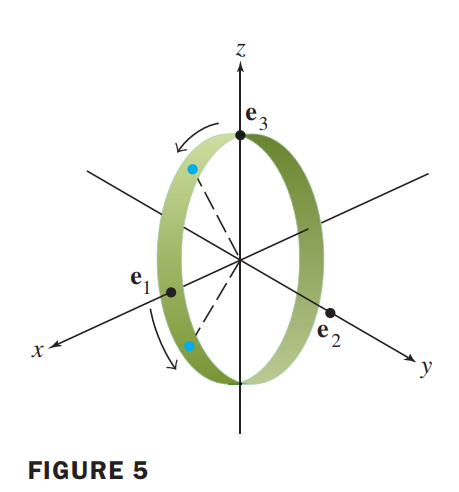
Rotation about the y-axis through an angle of 30°
Solution:
First, construct the $3\times 3$ matrix for the rotation.
The vector $\vec{e_1}$ rotates down toward the negative $z-axis$, stopping at $(\cos 30, 0, -\sin 30) = (\frac{\sqrt{3}}{2}, 0 , -0.5)$.
The vector $\vec{e_2}$ on the y-axis does not move.
The vector $\vec{e_3}$ on the $z-axis$ rotates down toward the positive $x-axis$, stopping at $(\sin 30, 0, \cos 30) = (0.5, 0, \frac{\sqrt{3}}{2})$. So the rotation matrix is
$$
\begin{bmatrix}
\frac{\sqrt{3}}{2} & 0 & 0.5\\
0 & 1 & 0\\
-0.5 & 0 & \frac{\sqrt{3}}{2}
\end{bmatrix}
$$
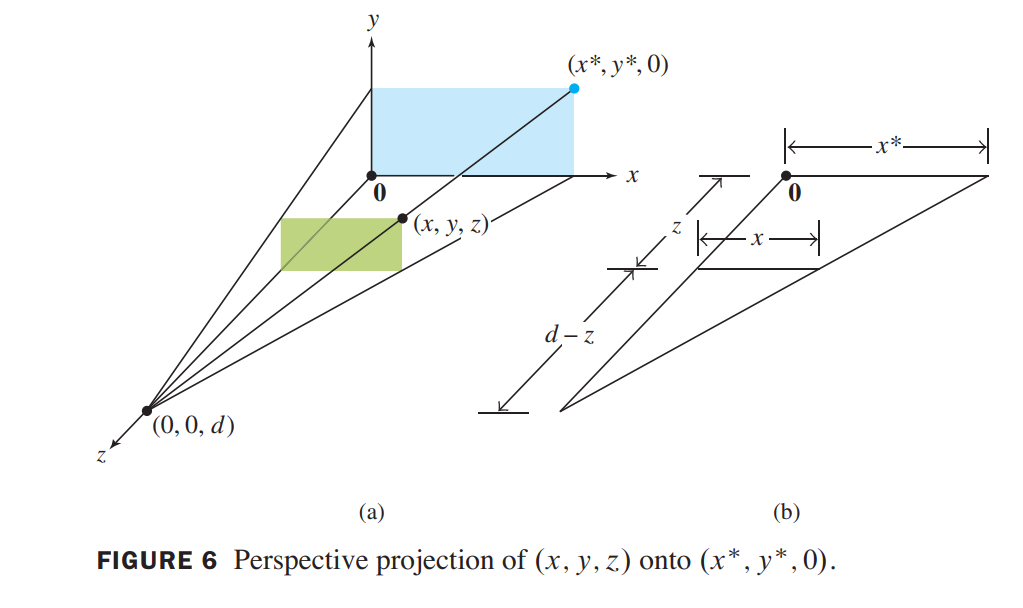
Perspective Projections
💡For example💡:
let $xy-plane$ represent the computer screen, and imagine that the eye of a viewer is along the positive $z-axis$, at point $(0,0,d)$.A perspective projection maps each point $(x,y,z)$ onto an image point $(x^{\ast}, y^{\ast}, 0)$.
Solution:
induce projection-matrix as follows:
$$
\frac{x^{\ast}}{d} = \frac{x}{d-z}
\rightarrow
x^{\ast} = \frac{dx}{d-z} = \frac{x}{1-\frac{z}{d}}
$$
$$
Similarly\rightarrow y^{\ast} = \frac{y}{1-\frac{z}{d}}
$$
$$
(x,y,z,1)\xrightarrow{projection} (\frac{x}{1-\frac{z}{d}}, \frac{y}{1-\frac{z}{d}}, 0 ,1)\sim(x,y,0,1-\frac{z}{d})
$$
$$
p\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
=
\begin{bmatrix}1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & -1/d & 1\end{bmatrix}\begin{bmatrix}x \\ y \\ z \\ 1 \end{bmatrix}
=
\begin{bmatrix}x \\ y \\ 0 \\ 1-\frac{z}{d}\end{bmatrix}
$$
👉More about Rotation matrix & Perspective projection >>
SubSpace of $R^n$
A subspace of $R^n$ is any set $H$ in $R^n$ that has three properties:
- The Zero Vector is in $H$.
- For each $\vec{u}$ and $\vec{v}$ in $H$, the sum $\vec{u} + \vec{v}$ is in $H$.
- For each $\vec{u}$ in $H$ and each scalar $c$, the vector $c\vec{u}$ is in $H$.
Column Space and Null Space of a Matrix
The column space of a matrix $A$ is the set $ColA$ of all linear combinations of the columns of $A$.
if $A = \begin{bmatrix}\vec{a_1} & \cdots & \vec{a_n}\end{bmatrix}$, with the columns in $R^m$, then $Col A$ is the same as $Span \set{\vec{a_1} \cdots \vec{a_n}}$.
💡For example💡:
Let A = $\begin{bmatrix}
1 & -3 & -4 \\
-4 & 6 & -2 \\
-3 & 7 & 6
\end{bmatrix}$ and b = $\begin{bmatrix}
3 \\
3 \\
-4
\end{bmatrix}$. Determine whether $\vec{b}$ is in the column space of $A$.
Solution:
$$
\begin{bmatrix}
1 & -3 & -4 & 3\\
-4 & 6 & -2 & 3\\
-3 & 7 & 6 & -4
\end{bmatrix}
\sim
\begin{bmatrix}
1 & -3 & -4 & 3\\
0 & -6 & -18 & 15\\
0 & 0 & 0 & 0
\end{bmatrix}
\\
有解,意味着b是A列向量的线性组合
\therefore
b \subseteq Col A
$$
Basis for a Subspace
A basis for a subspace $H$ of $R^n$ is a linearly independent set in $H$ that spans $H$.
$$
\vec{e_1} = \begin{bmatrix}
1 \\ 0 \\ \cdots \\ 0
\end{bmatrix},
\vec{e_2} = \begin{bmatrix}
0 \\ 1 \\ \cdots \\ 0
\end{bmatrix},
\cdots,
\vec{e_n} = \begin{bmatrix}
0 \\ 0 \\ \cdots \\ 1
\end{bmatrix}
$$
the set {$\vec{e_1}, \cdots, \vec{e_n}$} is called the standard basis for $R^n$.
💡For example💡:
Find a basis for the null space of the matrix.
$$
A = \begin{bmatrix}
-3 & 6 & -1 & 1 & -7\\
1 & -2 & 2 & 3 & -1\\
2 & -4 & 5 & 8 & -4
\end{bmatrix}
$$
找到矩阵零空间的一组基如下:
$$
\begin{bmatrix}A & \vec{0}\end{bmatrix}
\sim
\begin{bmatrix}
1 & -2 & 0 & -1 & 3 & 0\\
0 & 0 & 1 & 2 & -2 & 0\\
0 & 0 & 0 & 0 & 0 & 0
\end{bmatrix},
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
x_4\\
x_5
\end{bmatrix}=
\begin{bmatrix}
2x_2 + x_4 - 3x_5\\
x_2\\
-2x_4 + 2x_5\\
x_4\\
x_5
\end{bmatrix}=
x_2\begin{bmatrix}
2\\
1\\
0\\
0\\
0\\
\end{bmatrix} + x4\begin{bmatrix}
1\\
0\\
-2\\
1\\
0
\end{bmatrix} + x_5\begin{bmatrix}
-3\\
0\\
2\\
0\\
1
\end{bmatrix}
= x_2\vec{u} + x_4\vec{v} + x_5\vec{w}
\\
{\vec{u}, \vec{v}, \vec{w}} 是基向量
$$
Dimension and Rank
👉More About Dimension and Rank is in C4 >>
Coordinate Systems
Suppose the set $\beta = \set{\vec{b_1},\cdots\cdots, \vec{b_p}}$ is a basis for a SubSpace $H$. For each $\vec{x}$ in $H$, the coordinates of $\vec{x}$ relative to the basis $\beta$ are the weights $c_1, \cdots, c_p$ such that $\vec{x} = c_1\vec{b_1} + \cdots + c_p\vec{b_p}$, and the vector in $R^p$
$$
[\vec{x}]_\beta =
\begin{bmatrix}
c_1\\\cdots\\c_p
\end{bmatrix}
$$
is called the coordinate vector of $\vec{x}$(relative to $\beta$) or the $\beta-$ coordinate vector of $\vec{x}$
The Dimension of a Subspace
The rank of a matrix $A$, denoted by $rank A$, is the dimension of the column space of $A$
Determin the rank of the matrix
$$
A\sim
\begin{bmatrix}
2 & 5 & -3 & -4 & 8\\
0 & -3 & 2 & 5 & -7\\
0 & 0 & 0 & 4 & -6\\
\end{bmatrix}
矩阵有3个pivot-columns,所以rankA = 3
$$
If a matrix $A$ has $n$ columns, then $rank A + dim Nul A = n$.
Rank and the Invertible Matrix Theorem
Let $A$ be an $n \times n$ matrix. Then the following statements are each equivalent to the statement that $A$ is an invertible matrix.
m. The columns of $A$ form a basis of $R^n$:
n. $Col A = R^n$
o. $dim Col A = n$
p. $rank A = n$
q. $Nul A = {0}$
r. $dim Nul A = 0$

