Keywords: Newbie, Variation
This is the translation of this article(partly) https://zhuanlan.zhihu.com/p/139018146.
Basic Theory
Suppose we have two points $(a,p), (b,q)$, any curves joints them satisfies the bouding condition as follows:
$$
y(a) = p, y(b) = q
\tag{1}
$$
Now we consider the definite Integral:
$$
I = \int_a^b f(y,y’)dx
\tag{2}
$$
$f(y,y’)$ is a function about $y(x)$ and it’s first-order derivative $y’(x)$, we expect a specific $y(x)$ lets $I$ has extrema.
Recall what we have leanred about extrema in common function ? 👉More about Extrema >>
So $I$ is a functional(泛函) to $y(x)$ —- $y(x)$ changes, so as $I$, when $y(x) = ?$, I reaches the extrema.
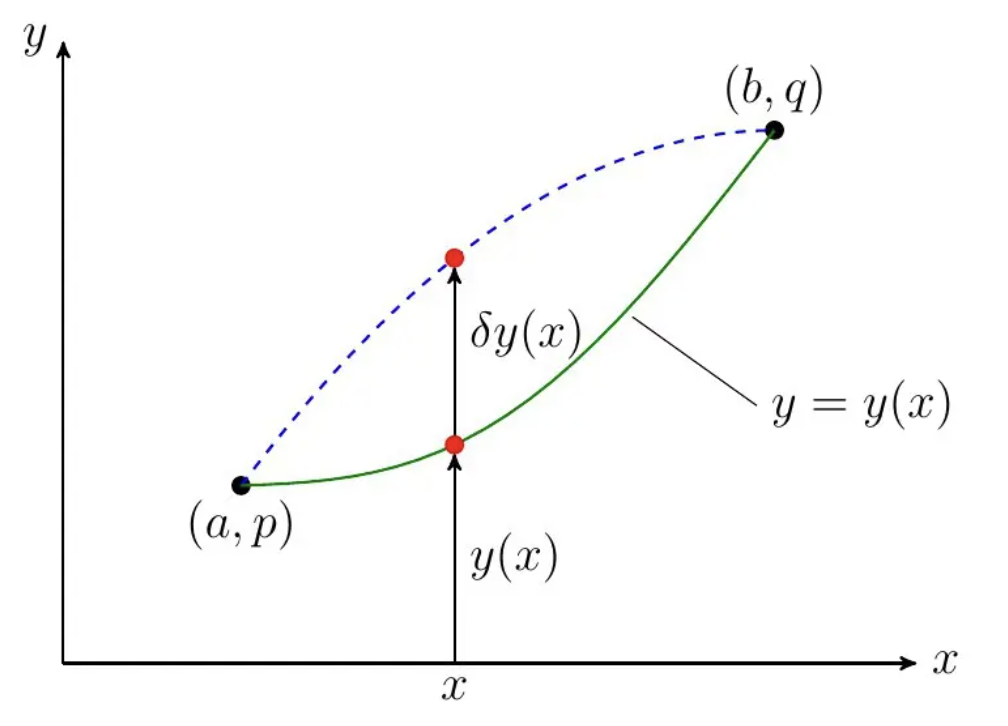
if y(x) has any small changes $\delta y(x)$, we call it the variation of $y(x)$. (In basic calculus, we denote the samll changes of $x$ is $\Delta x$ or $dx$)
So the changes of $f(y,y’)$ is:
$$
\delta f = \frac{\partial f}{\partial y} \delta y + \frac{\partial f}{\partial y’}\delta y’
\tag{3}
$$
👉More about Partial Calculus >>
The corresponding change of $I$ is :
$$
\begin{aligned}
\delta I &= \int_a^b (\delta f) dx \\
&= \int_a^b [\frac{\partial f}{\partial y} \delta y + \frac{\partial f}{\partial y’}\delta y’] dx \\
&= \int_a^b \frac{\partial f}{\partial y} \delta y dx + \int_a^b \frac{\partial f}{\partial y’}\delta y’ dx
\end{aligned}
\tag{4}
$$
the second term of equation(4) can be written as
$$
\frac{\partial f}{\partial y’}\delta y’ = \frac{\partial f}{\partial y’} \frac{d(\delta y)}{dx}
$$
so, we are going to simplify equation(4), we firstly integrate the second term:
$$
\begin{aligned}
\int_a^b \frac{\partial f}{\partial y’}\delta y’ dx &= \int_a^b \frac{\partial f}{\partial y’} \frac{d(\delta y)}{dx} dx\\
&= \int_a^b \frac{\partial f}{\partial y’} d(\delta y)\\
&= \left. \frac{\partial f}{\partial y’} \delta y \right|_a^b - \int_a^b \delta y d(\frac{\partial f}{\partial y’})\\
&= \left. \frac{\partial f}{\partial y’} \delta y \right|_a^b - \int_a^b \delta y \frac{d}{dx}(\frac{\partial f}{\partial y’}) dx\\
\end{aligned}
\tag{4.2}
$$
👉More about Integral Formulas >>
Since the function $y(x)$ has constant bouding value, which is $y(a) = p, y(b) = q$, so that
$$
\delta y(a) = 0, \delta y(b) = 0
$$
thus, the first term in Equation(4.2), $\left. \frac{\partial f}{\partial y’} \delta y \right|_a^b = 0$. Substitue (4.2) to (4), we get
$$
\begin{aligned}
\delta I &= \int_a^b \frac{\partial f}{\partial y} \delta y dx - \int_a^b \delta y \frac{d}{dx}(\frac{\partial f}{\partial y’}) dx \\
&= \int_a^b \left[ \frac{\partial f}{\partial y} - \frac{d}{dx}(\frac{\partial f}{\partial y’})\right] \delta y(x) dx
\end{aligned}
\tag{5}
$$
If $I$ has any extrama, then for any $\delta y(x)$ satisfying the bounding contitions, there must have $\delta I = 0$, which means:
$$
\frac{\partial f}{\partial y} - \frac{d}{dx}(\frac{\partial f}{\partial y’}) = 0
\tag{6}
$$
This is Euler-Lagrange Equation, which is the basic Theorem in Variation. With it, we can find the extremal funtion $y(x)$.
Of couse, Equation(6) is a second-order Differential function.
👉More about Second-Order Differential Functions >>
Examples
The shortest path between two points
Give two points in the xy-plane, which is the shortest path(curve) that joints them?
Solution:

