Animation-C14-Skinning

Keywords: Skinning, LBS, DQS, python

This is the ReadingNotes from video games105.

Skinning Definition

关于Rigging和Skinning的definition
Rigging: 创建一个控制器，通过控制器可以带来表情等的变化
Skinning：Rigging的特例，一般是针对骨骼动画

rigging-skinning

Skinning Deformation

LBS

The following figure describes basic idea of Linear Blend Skinning (LBS).

Bind Pose Definition
将骨骼和蒙皮绑定，计算这时候顶点在骨骼坐标系下的坐标表示，在图中用r来表示了

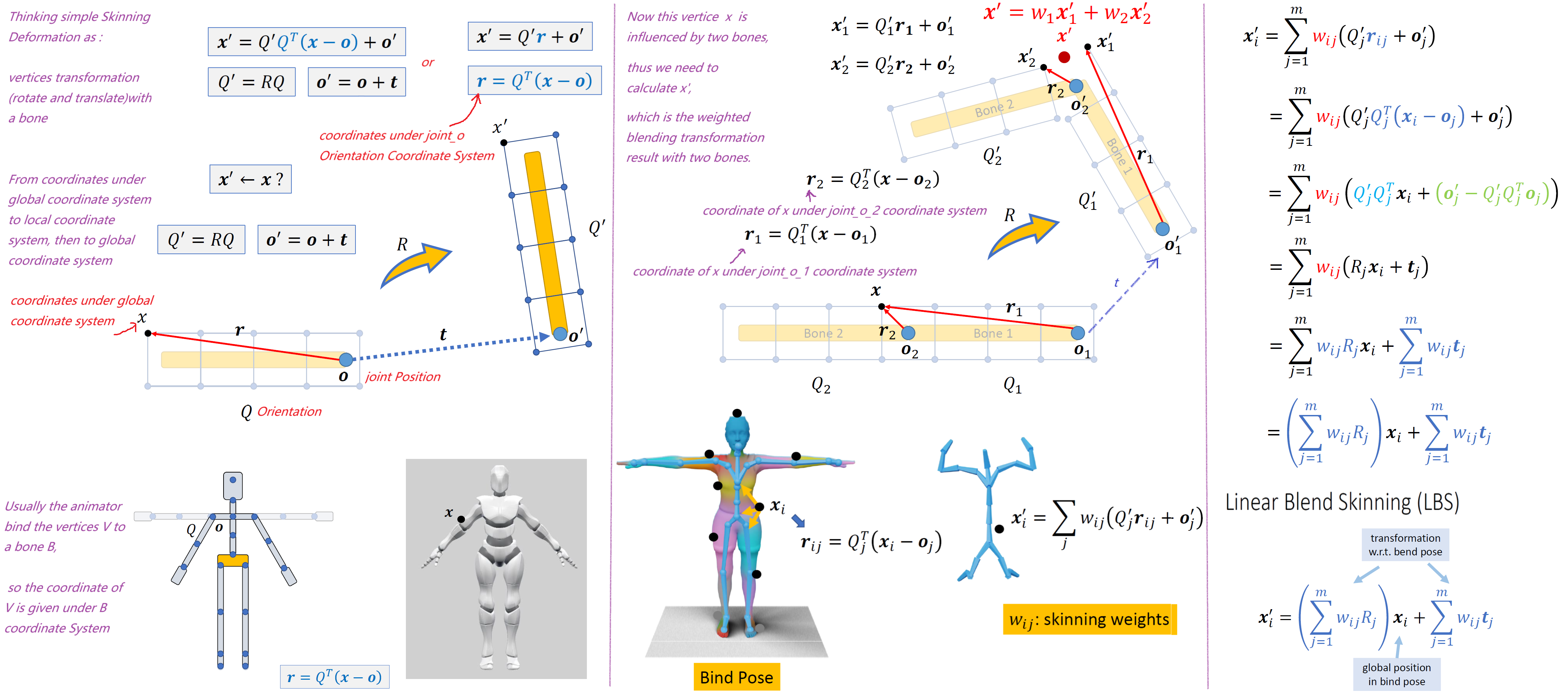
skinning-deformation

Bind Pose 和 T Pose
对于T-pose来讲，一般认为所有关节点的局部坐标系和global coordinate system一样
但Bind Pose可能不是T-Pose,是A-Pose，这时候的关节点的局部坐标系是有旋转的

一般情况下，我们约束一个顶点最多受到4个骨骼的影响。

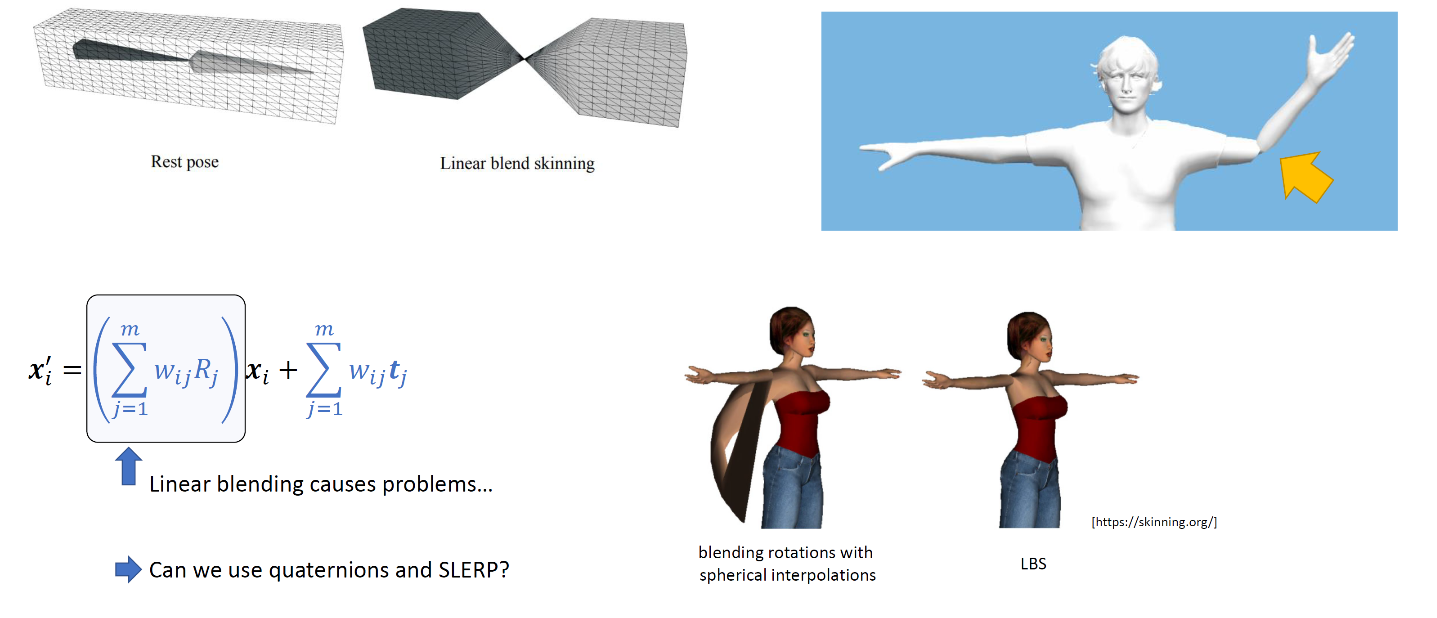
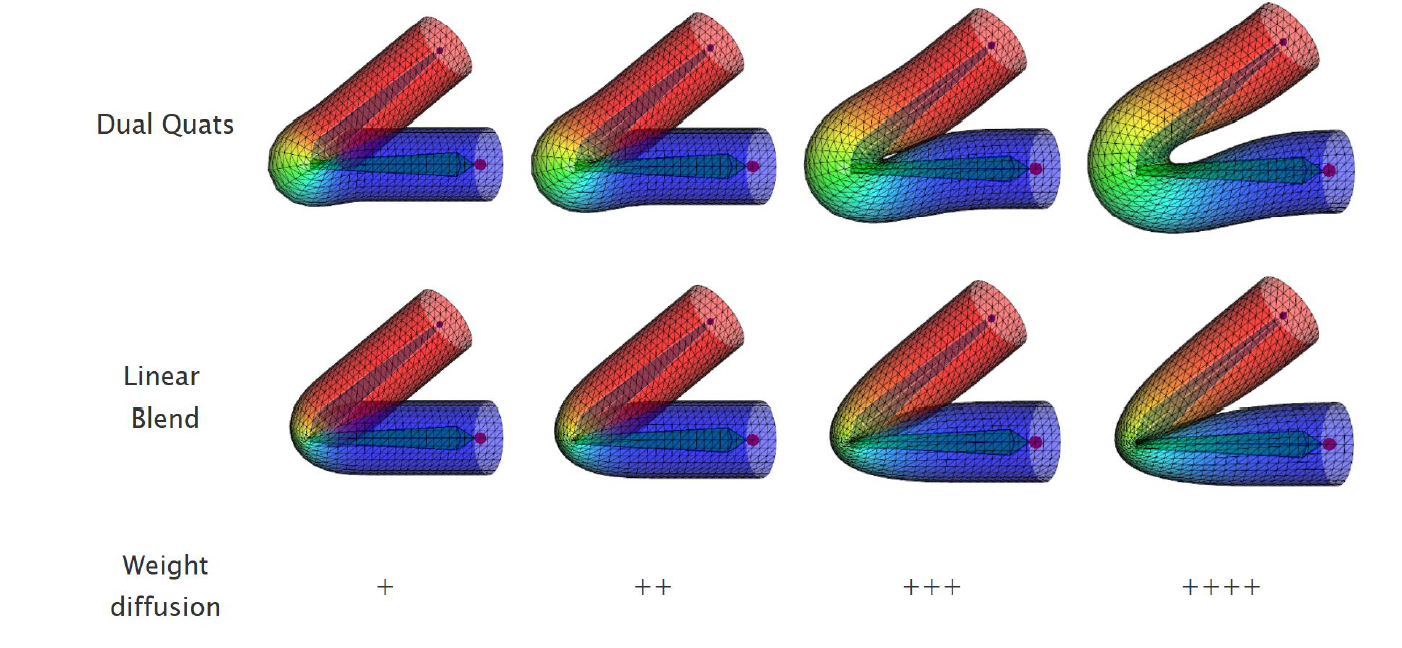
Candy Wrapper Artifact

Since LBS is linear Blending Skinning, it has the artifacts called Candy Wrapper Artifact.

—>Why LBS has candy wrapper artifact?
We all know that linear interpolate rotation matrix(which is orthogonal matrix) may get non-rotation matrix.
—>Can we use Quaternion slerp to solve candy wrapper artifact?
No, from the figure we can see quaternion slerp is no better than matrix interpolate, the reason is $R_j$ is a rotation around global coordinate system origin point. The blending of $R_j$ can not fit well with $t_j$

candy-wrapper

Automated Skinning

Latest research focuses on how to automatically calculate the weights given a binding model:

[1]Learning Skeletal Articulations with Neural Blend Shapes_Siggraph_2021

[2]NeuroSkinning: Automatic Skinning Binding for Production Characters with Deep Graph Networks_Siggraph_2019

DQS

The following figure describes basic idea of Dual-Quaterninon Skinning (DQS).

DQS

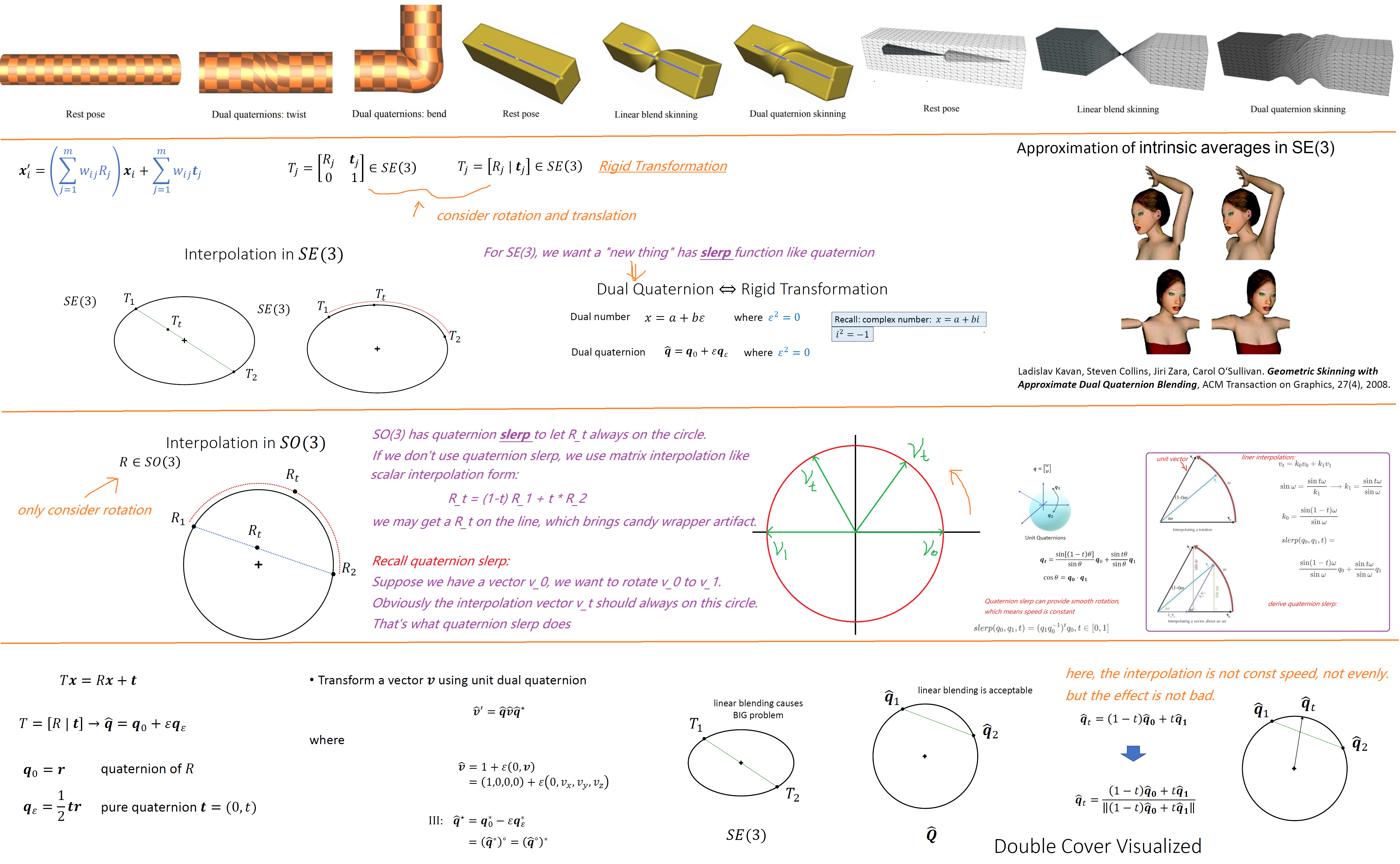
Dual Quaternion / Quaternion

What’s the difference between Dual Quaternion and Quaternion?

For Quaternion:

The unit vector $\pmb{\hat{n}}$ defines an axis of rotation, and the scalar $\theta$ is the amount of rotation about this axis.
$$
\begin{aligned}
\pmb{q} &= \begin{bmatrix}w & \pmb{v} \end{bmatrix}\\
&=\begin{bmatrix}\cos(\theta/2) & sin(\theta/2)\pmb{\hat{n}} \end{bmatrix}
\end{aligned}
$$

The quaternions $\pmb{q}$ and $-\pmb{q}$ describe the same angular displacement. Any angular displacement in 3D has exactly two distinct representations in quaternion format, and they are negatives of each other.
It’s not too difficult to see why this is true. If we add $360°$ to $\theta$, it doesn’t change the angular displacement represented by $q$, but it negates all four components of $q$.
$$
\begin{aligned}
-\pmb{q} &= -\begin{bmatrix}w & \pmb{v} \end{bmatrix}\\
&=\begin{bmatrix}-\cos(\theta/2) & -sin(\theta/2)\pmb{\hat{n}} \end{bmatrix}
\end{aligned}
$$

there are two “identity” quaternions that represent “no angular displacement.”
$$
\begin{bmatrix}1 & \pmb{0} \end{bmatrix}\\
\begin{bmatrix}-1 & \pmb{0} \end{bmatrix}
$$

Rotation quaternions have unit magnitude:
$$
\begin{aligned}
||q|| &= \sqrt{w^2 + ||\pmb{v}||^2}\\
&= \sqrt{\cos^2(\theta/2) + (\sin(\theta/2)||\pmb{\hat{n}}||)^2}\\
&= 1
\end{aligned}
$$

The conjugate of a quaternion, denoted $\pmb{q^\ast}$, is obtained by negating the vector portion of the quaternion
$$
\pmb{q^\ast} = \begin{bmatrix}w & -\pmb{v} \end{bmatrix}
$$

The inverse of a quaternion, denoted $\pmb{q}^{−1}$, is defined as the conjugate of a quaternion divided by its magnitude:
$$
\pmb{q}^{−1} = \frac{\pmb{q\ast}}{||\pmb{q}||}
$$

quaternion dot product
$$
\pmb{q_1q_2} = \begin{bmatrix}w_1w_2 - \pmb{v_1 \cdot v_2} & w_1\pmb{v_2} + w_2\pmb{v_1} + \pmb{v_1} \times \pmb{v_2}\end{bmatrix}
$$

dual-quaternion

Budging Artifact

budging

To Correct LBS

This method is pretty intuitive, we just need to add a delta value to vertice $p$ at binding stage, the basic idea is as follows:

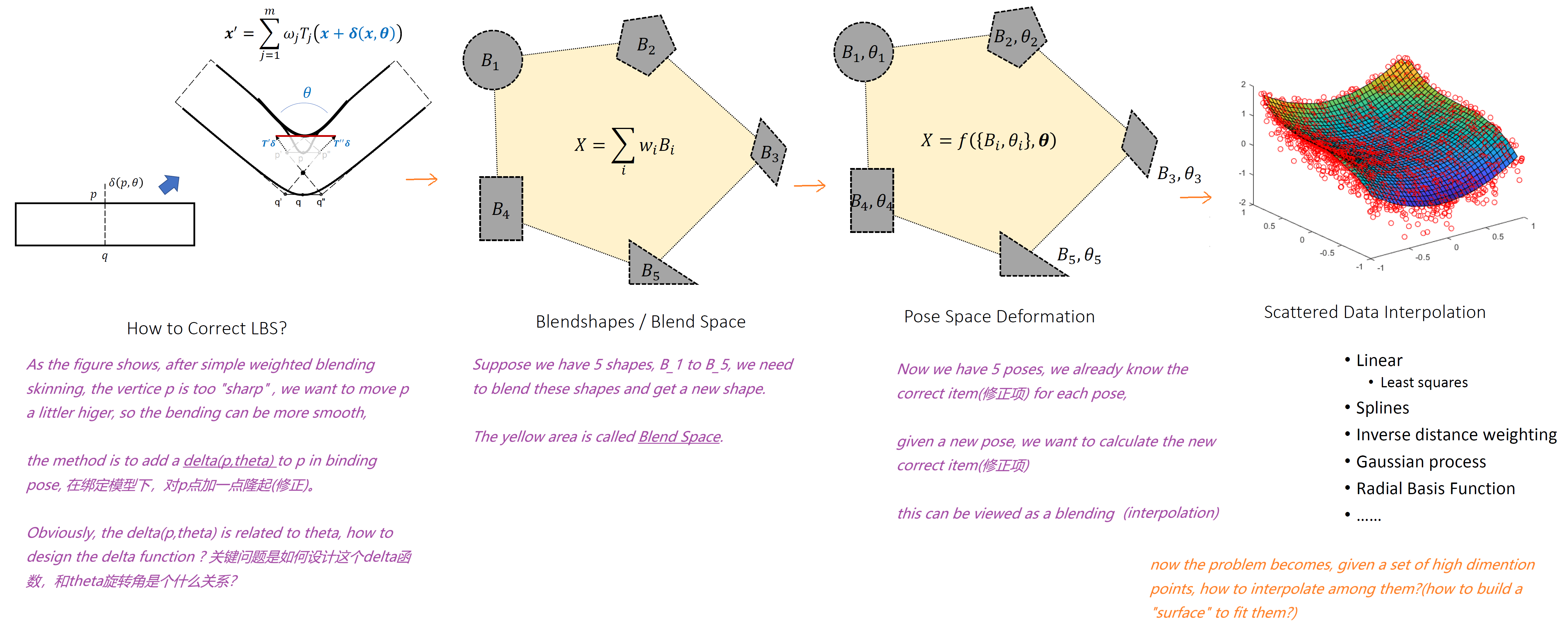
correct_lbs

RBF Interpolation

There are a lot of mothods to calculate interpolation among high dimension points, like Least Squares, Splines, Gaussian process, Radial Basis Function(径向基函数), new we introduce Radial Basis Function.

RBF-interpolation