Keywords: Variational Linear Regression, Variational Logistic Regression, Variational Inference, Python
This is the Chapter10 ReadingNotes from book Bishop-Pattern-Recognition-and-Machine-Learning-2006. [Code_Python]
👉Simply Understand Variational Inference >>
Variational Inference
Functional like entropy $H[p]$, which takes a probability distribution $p(x)$ as the input and returns the quantity:
$$
H[p] = \int p(x) \ln p(x) dx
\tag{10.1}
$$
as the output.
We can the introduce the concept of a functional derivative, which expresses how the value of the functional changes in response to infinitesimal changes to the input function.
Suppose we have a fully Bayesian model in which all parameters are given prior distributions.
Our probabilistic model specifies the joint distribution $p(\pmb{X},\pmb{Z})$, and our goal is to find an approximation for the posterior distribution $p(\pmb{Z}|\pmb{X})$ as well as for the model evidence $p(X)$.

As before, we can maximize the lower bound $\mathcal{L}(q)$ by optimization with respect to the distribution $q(\pmb{Z})$, which is equivalent to minimizing the $KL$ divergence. If we allow any possible choice for $q(\pmb{Z})$, then the maximum of the lower bound occurs when the $KL$ divergence vanishes, which occurs when $q(\pmb{Z})$ equals the posterior distribution $p(\pmb{Z}|\pmb{X})$.
However, in practice, $p(\pmb{Z}|\pmb{X})$ is intractable.
We therefore consider instead a restricted family of distributions $q(\pmb{Z})$ and then seek the member of this family for which the $KL$ divergence is minimized.
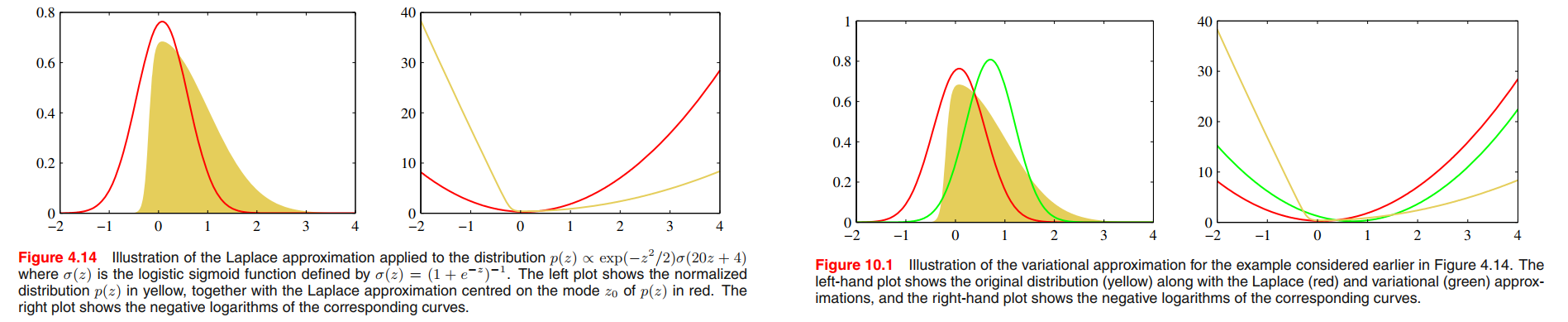
One way to restrict the family of approximating distributions is to use a parametric distribution $q(\pmb{Z}|\pmb{\omega})$ governed by a set of parameters $\omega$. The lower bound $L(q)$ then becomes a function of $\omega$, and we can exploit standard nonlinear optimization techniques to determine the optimal values for the parameters.

