Keywords: Cycloids, Brachistochrones(最速降线), Parametric Curves
This is the Chapter11 ReadingNotes from book Thomas Calculus 14th.
Parametrizations of Plane Curves
Parametric Equations
Definition
If $x$ and $y$ are given as functions
$$
x = f(t), y = g(t)
$$
over an interval $I$ of $t$-values, then the set of points $(x, y) = (ƒ(t), g(t))$ defined by these equations is a parametric curve. The equations are parametric equations for the curve.
Cycloids(摆线)
💡For example💡:
A wheel of radius a rolls along a horizontal straight line. Find parametric equations for the path traced by a point $P$ on the wheel’s circumference. The path is called a cycloid.
Solution:
We take the line to be the $x$-axis, mark a point $P$ on the wheel, start the wheel with $P$ at the origin, and roll the wheel to the right. As parameter, we use the angle $t$ through which the wheel turns, measured in radians. Figure 11.9 shows the wheel a short while later when its base lies at units from the origin. The wheel’s center $C$ lies at $(at, a)$ and the coordinates of $P$ are
$$
x = at + a \cos \theta, y = a + a \sin \theta
$$
To express $\theta$ in terms of $t$, we observe that $t + \theta = \frac{3\pi}{2}$ in the figure, so that
$$
\theta = \frac{3\pi}{2} - t
$$
This makes
$$
\cos\theta = -\sin t, \sin \theta = -\cos t
$$
The equations we seek are
$$
x = at - a \sin t, y = a(1-\cos t)
$$
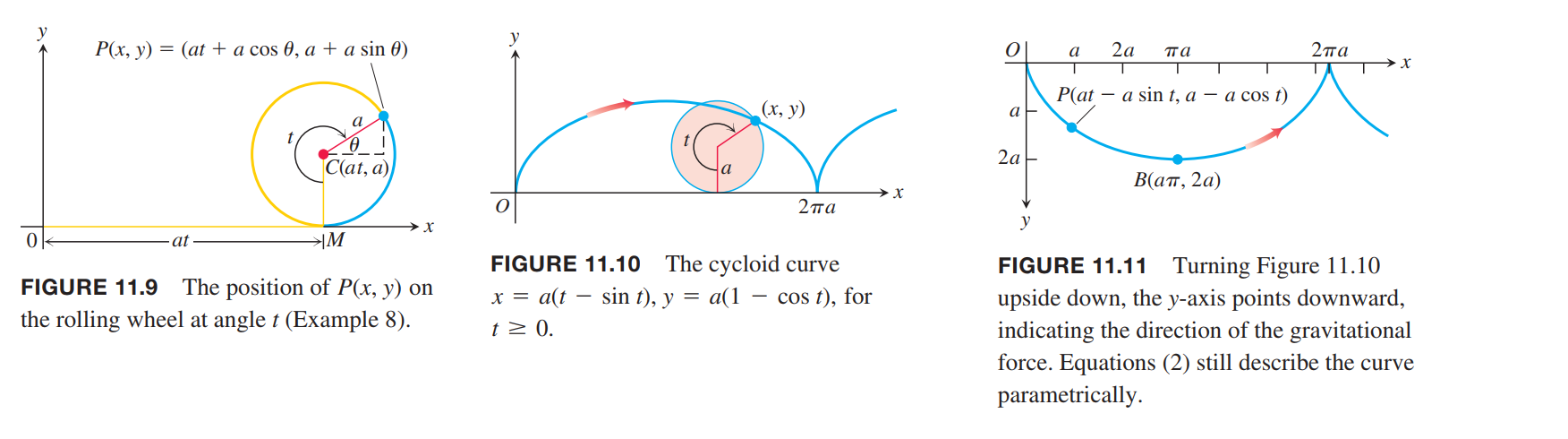
Brachistochrones(最速降线) and Tautochrones(等时曲线)
two properties:
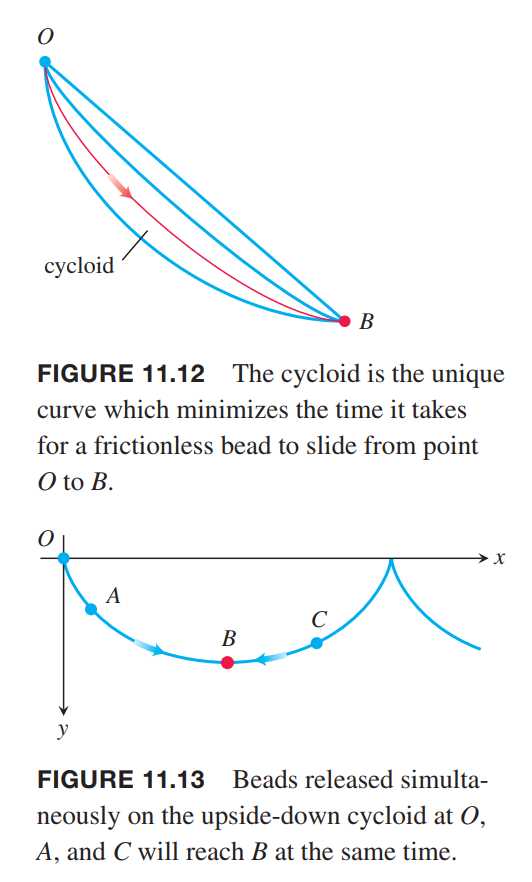
- Among all smooth curves joining these points, the cycloid is the curve along which a frictionless bead, subject only to the force of gravity, will slide from $O$ to $B$ the fastest. This makes the cycloid a brachistochrone (“brah-kiss-toe-krone”), or shortest-time curve for these points.
- even if you start the bead partway down the curve toward $B$, it will still take the bead the same amount of time to reach $B$. This makes the cycloid a tautochrone (“taw-toe-krone”),or same-time curve for $O$ and $B$.
Are there any other brachistochrones joining $O$ and $B$, or is the cycloid the only one?
We can formulate this as a mathematical question in the following way.
At the start, the kinetic energy of the bead is zero, since its velocity (speed) is zero. The work done by gravity in moving the bead from $(0, 0)$ to any other point $(x, y)$ in the plane is $mgy$, and this must equal the change in kinetic energy. That is,
$$
mgy = \frac{1}{2}mv^2 - \frac{1}{2}m(0)^2
$$
Thus, the speed of the bead when it reaches $(x, y)$ has to be $v = \sqrt{2gy}$. That is,
$$
\frac{ds}{dT} = \sqrt{2gy}, s: arc-length, T: time
$$
or
$$
dT = \frac{ds}{\sqrt{2gy}} = \frac{\sqrt{1+(dy/dx)^2}dx}{\sqrt{2gy}}
$$
The time $T_ƒ$ it takes the bead to slide along a particular path $y = ƒ(x)$ from $O$ to $B(a\pi, 2a)$ is
$$
T_f = \int_{x=0}^{x=a\pi} \sqrt{\frac{1+(dy/dx)^2}{2gy}}dx
$$
What curves $y = ƒ(x)$, if any, minimize the value of this integral?
👉More about Calculus of Variations >>
Calculus with Parametric Curves
Tangents and Areas
A parametrized curve $x = ƒ(t)$ and $y = g(t)$ is differentiable at $t$ if $ƒ$ and $g$ are differentiable at $t$.
At a point on a differentiable parametrized curve where $y$ is also a differentiable function of $x$ follows the Chain Rule:
$$
\frac{dy}{dt} = \frac{dy}{dx} \cdot \frac{dx}{dt}
$$
Parametric Formula for $dy/dx$
If all three derivatives exist and $dx/dt \neq 0$, then
$$
\frac{dy}{dt} = \frac{dy/dt}{dx/dt}
\tag{1}
$$
If parametric equations define $y$ as a twice-differentiable function of $x$, then
$$
\frac{d^2y}{d^2x} = \frac{d}{dx}y’ = \frac{d’y/dt}{dx/dt}
$$
Length of a Parametrically Defined Curve
We assume the functions $ƒ$ and $g$ are continuously differentiable, the derivatives $ƒ’(t)$ and $g’(t)$ are not simultaneously zero, which prevents the curve $C$ from having any corners or cusps. Such a curve is called a smooth curve.
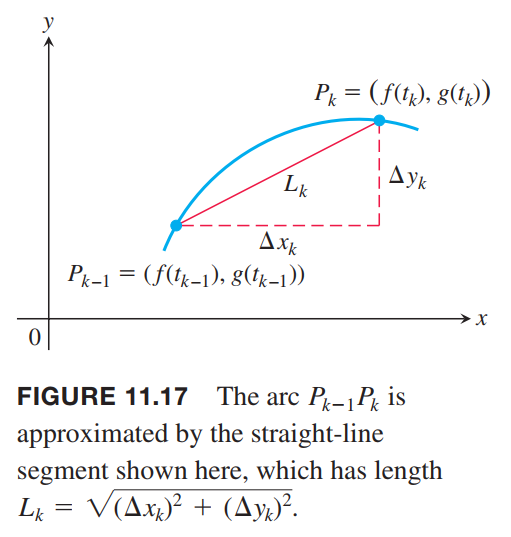
$$
\begin{aligned}
L_k &= \sqrt{(\Delta x_k)^2 + (\Delta y_k)^2}\\
&= \sqrt{[f(t_k) - f(t_{k-1})]^2 + [g(t_k) - g(t_{k-1})]^2}
\end{aligned}
$$
By the Mean Value Theorem there are numbers $t_k^\ast$ and $t_k^{\ast\ast}$ in $[t_{k-1}, t_{k}]$ such that
$$
\Delta x_k = f(t_k) - f(t_{k-1}) = f’(t_k^\ast)\Delta t_k
$$
$$
\Delta y_k = g(t_k) - g(t_{k-1}) = g’(t_k^{\ast\ast})\Delta t_k
$$
thus,
$$
\begin{aligned}
\sum_{k=1}^{n} L_k &= \sum_{k=1}^{n}\sqrt{[f’(t_k^\ast)\Delta t_k]^2 + [g’(t_k^{\ast\ast})\Delta t_k]^2}\\
&= \sum_{k=1}^{n}\sqrt{[f’(t_k^\ast)]^2 + [g’(t_k^{\ast\ast})]^2} \Delta t_k
\end{aligned}
$$
Although this last sum on the right is not exactly a Riemann sum (because $ƒ’$ and $g’$ are evaluated at different points), it can be shown that its limit, as the norm of the partition tends to zero and the number of segments $n \rightarrow \infty$, is the definite integral
$$
\lim_{||P|| \rightarrow 0} \sum_{k=1}^{n}\sqrt{[f’(t_k^\ast)]^2 + [g’(t_k^{\ast\ast})]^2} \Delta t_k =
\int_a^b \sqrt{[f’(t)]^2 + [g’(t)]^2}dt
$$
Definition
If a curve $C$ is defined parametrically by $x = ƒ(t)$ and $y = g(t)$, $a \leq t \leq b$, where $ƒ’$ and $g’$ are continuous and not simultaneously zero on $[a,b]$, and $C$ is traversed exactly once as $t$ increases from $t = a$ to $t = b$, then the length of $C$ is the definite integral
$$
L = \int_a^b \sqrt{[f’(t)]^2 + [g’(t)]^2} dt
\tag{3}
$$
Length of a Curve $y = ƒ(x)$
$$
x = t, y = f(t), a \leq t \leq b
$$
thus,
$$
\frac{dx}{dt} = 1, \frac{dy}{dt} = f’(t)
$$
thus,
$$
L = \int_a^b \sqrt{1 + [f’(x)]^2} dx
$$
The Arc Length Differential
$$
ds = \sqrt{dx^2 + dy^2}
$$
To be added…

