Keywords: Vector Functions, Curves, Tangents, Normal Vectors
This is the Chapter13 ReadingNotes from book Thomas Calculus 14th.
Curves in Space and Their Tangents
We use the calculus of these functions to describe the paths and motions of objects moving in a plane or in space, so their velocities and accelerations are given by vectors.
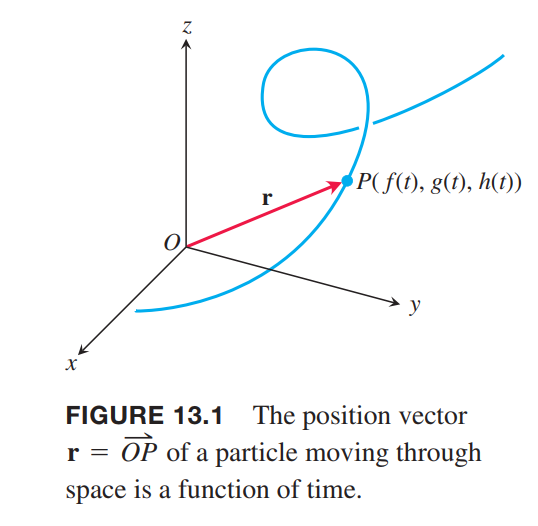
A curve in space can also be represented in vector form. The vector
$$
\vec{r(t)} = \vec{OP} = f(t)\vec{i} + g(t)\vec{j} + h(t)\vec{k}
\tag{2}
$$
Limits and Continuity
DEFINITION
Let $\vec{r(t)} = f(t)\vec{i} + g(t)\vec{j} + h(t)\vec{k}$ be a vector function with domain $D$, and let $\vec{L}$ be a vector. We say that $\vec{r}$ has limit $\vec{L}$ as $t$ approaches $t_0$ and write
$$
\lim_{t\rightarrow t_0} \vec{r(t)} = \vec{L}
$$
if, for every number $\epsilon > 0$, there exists a corresponding number $\delta > 0$ such that for all $t \in D$
$$
|\vec{r(t)} - \vec{L}| < \epsilon, whenever, 0 < |t - t_0| < \delta
$$
DEFINITION
A vector function $\vec{r(t)}$ is continuous at a point $t = t_0$ in its domain if $\lim_{t \rightarrow t_0} \vec{r(t)} = \vec{r(t_0)}$. The function is continuous if it is continuous at every point in its domain.
Derivatives and Motion
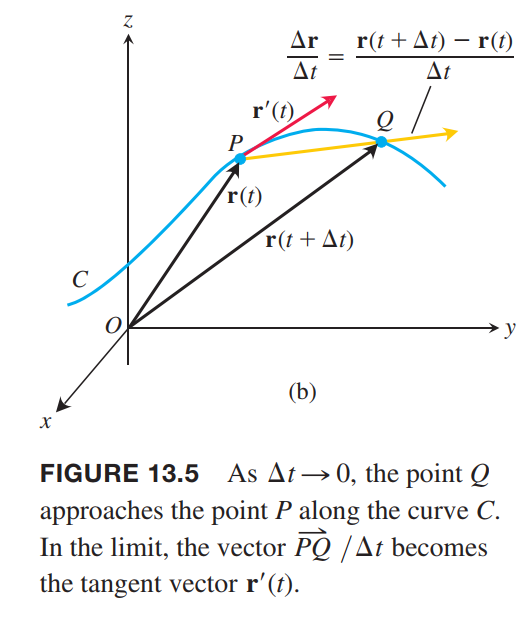
DEFINITION
The vector function $\vec{r(t)} = f(t)\vec{i} + g(t)\vec{j} + h(t)\vec{k}$ has a derivative (is differentiable) at $t$ if $ƒ, g, h$ have derivatives at $t$. The derivative is the vector function
$$
\begin{aligned}
\vec{r’(t)} &= \frac{d\vec{r}}{dt} \\
&= \lim_{\Delta t \rightarrow 0} \frac{\vec{r(t + \Delta t)} - \vec{r(t)}}{\Delta t} \\
&= \frac{df}{dt}\vec{i} + \frac{dg}{dt}\vec{j} + \frac{dh}{dt}\vec{k}
\end{aligned}
$$
DEFINITION
If $\vec{r}$ is the position vector of a particle moving along a smooth curve in space, then
$$
\vec{v(t)} = \frac{d\vec{r}}{dt}
$$
is the particle’s velocity vector, tangent to the curve. At any time $t$, the direction of $\vec{v}$ is the direction of motion, the magnitude of $\vec{v}$ is the particle’s speed, and the derivative $\vec{a} = d\vec{v}/dt$, when it exists, is the particle’s acceleration vector. In summary,
- Velocity is the derivative of position: $\vec{v} = \frac{d\vec{r}}{dt}$
- Speed is the magnitude of velocity: $Speed = |\vec{v}|$
- Acceleration is the derivative of velocity: $\vec{a} = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2}$
- The unit vector $\vec{v} / |\vec{v}|$ is the direction of motion at time $t$.
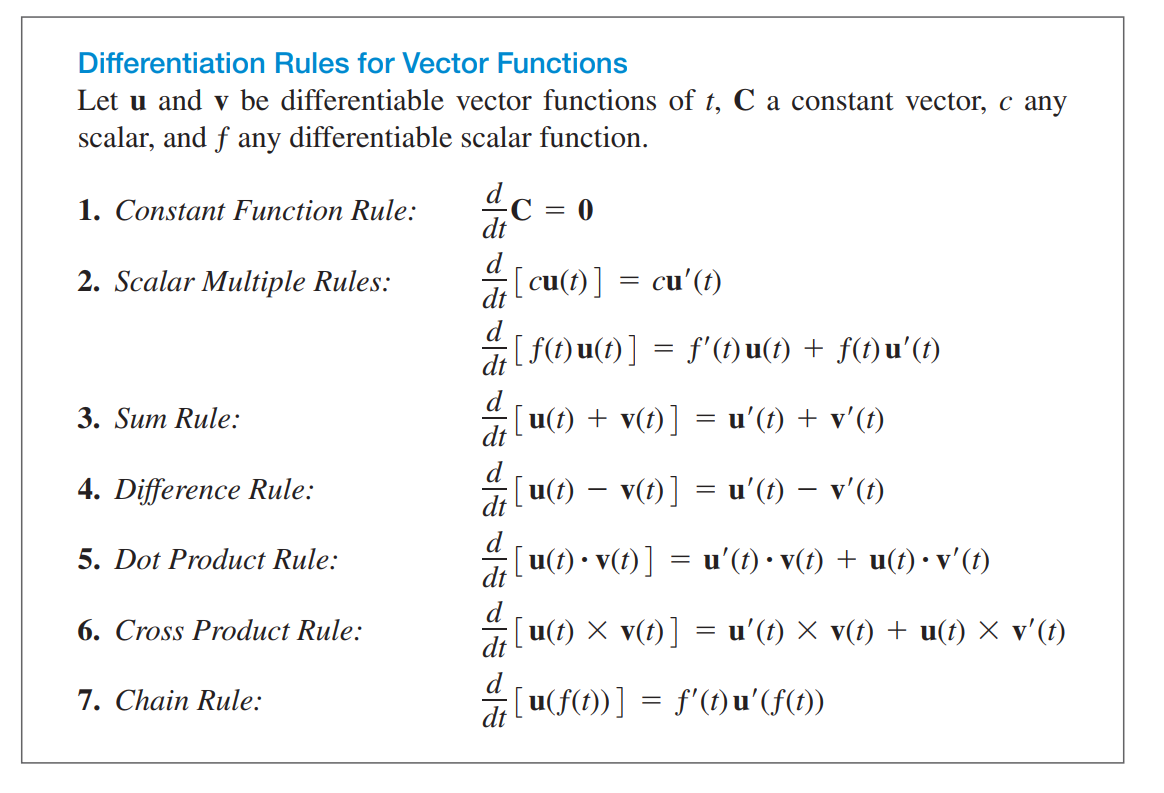
Differentiation Rules
Vector Functions of Constant Length
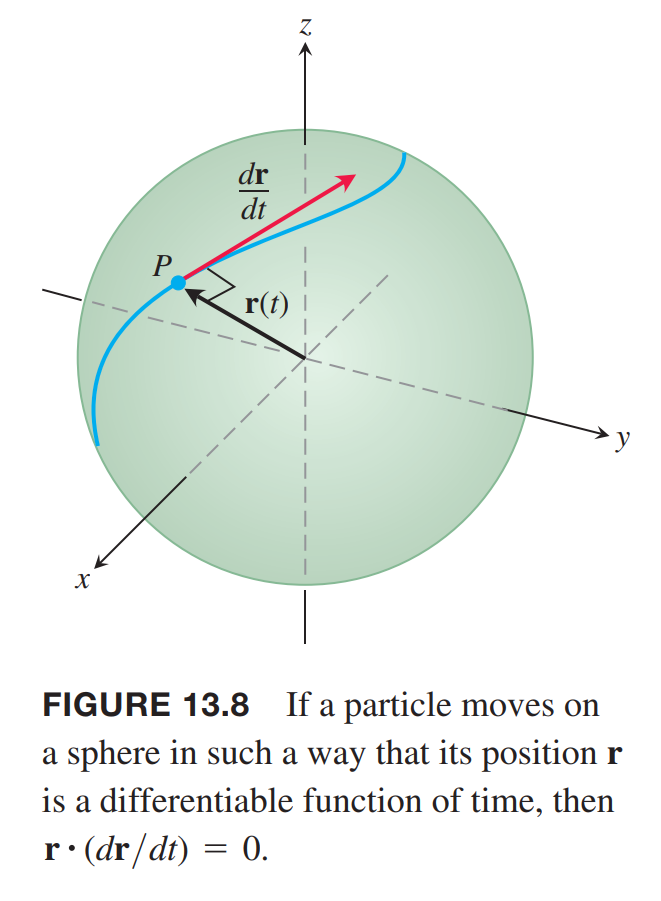
the position vector has a constant length equal to the radius of the sphere. The velocity vector $dr / dt$, tangent to the path of motion, is tangent to the sphere and hence perpendicular to $r$.
If $r$ is a differentiable vector function of $t$ and the length of $r(t)$ is constant, then
$$
r \cdot \frac{dr}{dt} = 0
\tag{4}
$$
Integrals of Vector Functions; Projectile Motion
Integrals of Vector Functions
DEFINITION
The indefinite integral of $\vec{r}$ with respect to $t$ is the set of all antiderivatives of $\vec{r}$, denoted by $\int \vec{r(t)} dt$. If $\vec{R}$ is any antiderivative of $\vec{r}$, then
$$
\int \vec{r(t)} dt = \vec{R(t)} + C
$$
DEFINITION
If the components of $r(t) = ƒ(t)i + g(t)j + h(t)k$ are integrable over $[a,b]$, then so is $r$, and the definite integral of $r$ from $a$ to $b$ is
$$
\int_a^b r(t) dt = \left( \int_a^b f(t) dt \right) i + \left( \int_a^b g(t) dt \right) j + \left( \int_a^b h(t) dt \right) k
$$
The Vector and Parametric Equations for Ideal Projectile Motion(抛射运动)
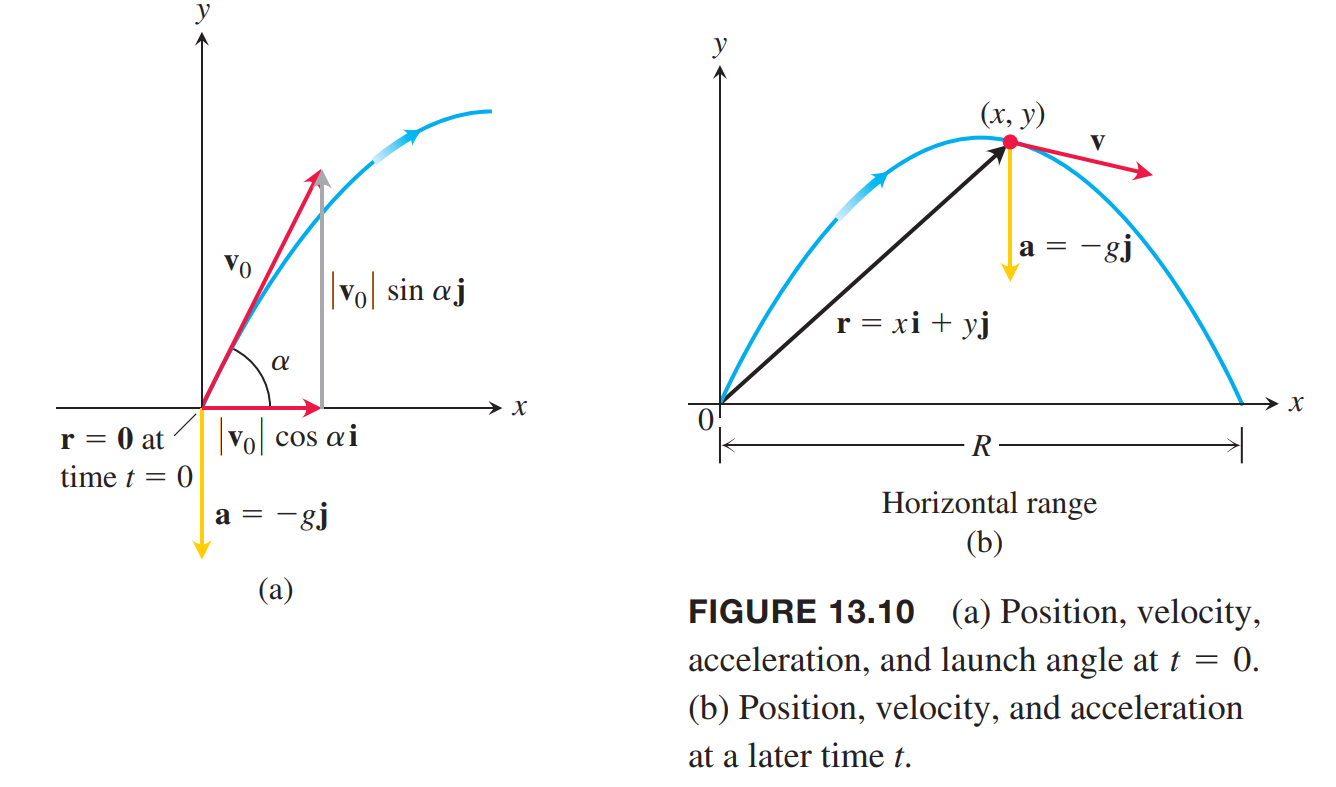
$$
\vec{v_0} = (|\vec{v_0}| \cos \alpha) \vec{i} + (|\vec{v_0}| \sin \alpha) \vec{j}
$$
use the simpler notation $v_0$ for the initial speed $\vec{v_0}$,
$$
\vec{v_0} = (v_0 \cos \alpha) \vec{i} + (v_0 \sin \alpha) \vec{j}
\tag{3}
$$
The projectile’s initial position is
$$
\vec{r_0} = 0\vec{i} + 0\vec{j} + 0\vec{k}
\tag{4}
$$
Newton’s second law of motion says that the force acting on the projectile is equal to the projectile’s mass $m$ times its acceleration, or $m(d^2\vec{r} / dt^2)$ if $\vec{r}$ is the projectile’s position vector and $t$ is time.
$$
m\frac{d^2\vec{r}}{dt^2} = -mg\vec{j}
$$
Thus, Differential equation:
$$
\frac{d^2\vec{r}}{dt^2} = -g\vec{j}
$$
Initial conditions:
$$
\vec{r} = \vec{r_0}, \frac{d\vec{r}}{dt} = \vec{v_0}, when \space t = 0
$$
The first integration gives:
$$
\frac{d\vec{r}}{dt} = -(gt)\vec{j} + \vec{v_0}
$$
A second integration gives:
$$
\vec{r} = -\frac{1}{2}gt^2\vec{j} + \vec{v_0}t + \vec{r_0}
$$
Substituting the values of $\vec{v_0}$ and $\vec{r_0}$ from Equations (3) and (4) gives
$$
\vec{r} = (v_0\cos \alpha) t \vec{i} + \left( (v_0\sin \alpha)t - \frac{1}{2}gt^2\right)\vec{j}
$$
Projectile Motion with Wind Gusts
Arc Length in Space
Arc Length Along a Space Curve
DEFINITION
The length of a smooth curve $r(t) = x(t)i + y(t)j + z(t)k$, $a \leq t \leq b$, that is traced exactly once as $t$ increases from $t = a$ to $t = b$, is
$$
\begin{aligned}
L &= \int_a^b \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2 + (\frac{dz}{dt})^2} dt \\
&= \int_a^b |\vec{v}| dt
\end{aligned}
\tag{1}
$$
If we choose a base point $P(t_0)$ on a smooth curve $C$ parametrized by $t$, each value of $t$ determines a point $P(t) = (x(t), y(t), z(t))$ on $C$ and a “directed distance”
$$
\begin{aligned}
s(t) &= \int_{t_0}^t \sqrt{[x’(\tau)]^2 + [y’(\tau)]^2 + [z’(\tau)]^2} d\tau\\
&= \int_{t_0}^{t} |\vec{v(\tau)}| d\tau
\end{aligned}
\tag{3}
$$
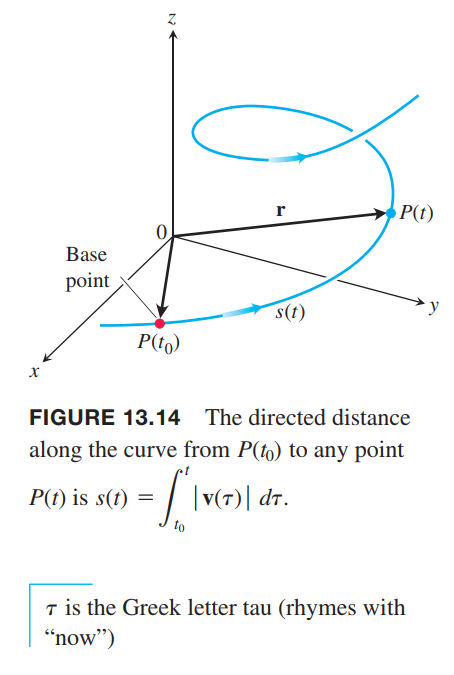
Recall the similar definition form in 👉Fundamental Theorem, Part 1 >>?
We call $s$ an arc length parameter for the curve.
We use the Greek letter $\tau$ (“tau”) as the variable of integration in Equation (3) because the letter $t$ is already in use as the upper limit.
Speed on a Smooth Curve
Since the derivatives beneath the radical in Equation (3) are continuous (the curve is smooth), the 👉Fundamental Theorem of Calculus tells us that $s$ is a differentiable function of $t$ with derivative
$$
\frac{ds}{dt} = |\vec{v(t)}|
\tag{4}
$$
Notice that $ds/dt > 0$ since, by definition, $|\vec{v}|$ is never zero for a smooth curve. We see once again that $s$ is an increasing function of $t$.
Unit Tangent Vector
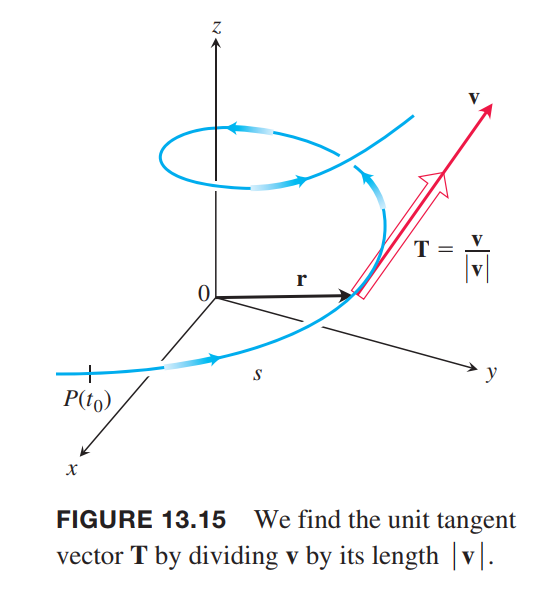
$$
\vec{T} = \frac{\vec{v}}{|\vec{v}|}
$$
The velocity vector is the change in the position vector $\vec{r}$ with respect to time $t$, but how does the position vector change with respect to arc length? More precisely, what is the derivative $d\vec{r}/ds$? Since $d\vec{s}/dt > 0$ for the curves we are considering, $s$ is one-to-one and has an inverse that gives $t$ as a differentiable function of $s$. The derivative of the inverse is
$$
\frac{dt}{ds} = \frac{1}{ds/dt} = \frac{1}{|\vec{v}|}
$$
This makes $\vec{r}$ a differentiable function of $s$ whose derivative can be calculated with the Chain Rule to be
$$
\frac{d\vec{r}}{ds} = \frac{d\vec{r}}{dt} \frac{dt}{ds} = \vec{v}\frac{1}{|\vec{v}|} = \frac{\vec{v}}{|\vec{v}|} = T
$$
Curvature and Normal Vectors of a Curve
Curvature of a Plane Curve
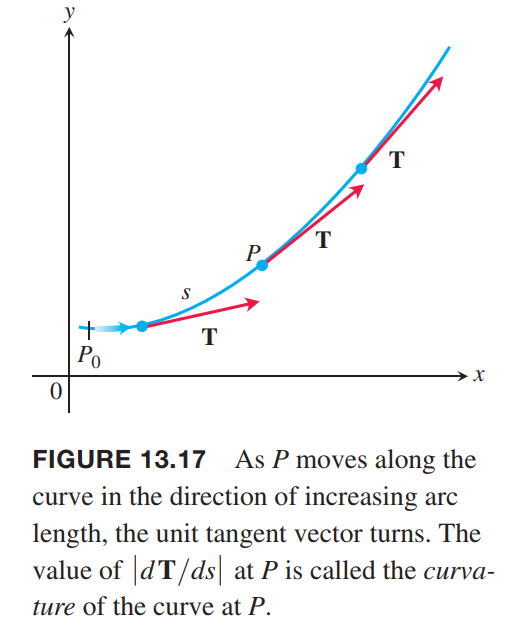
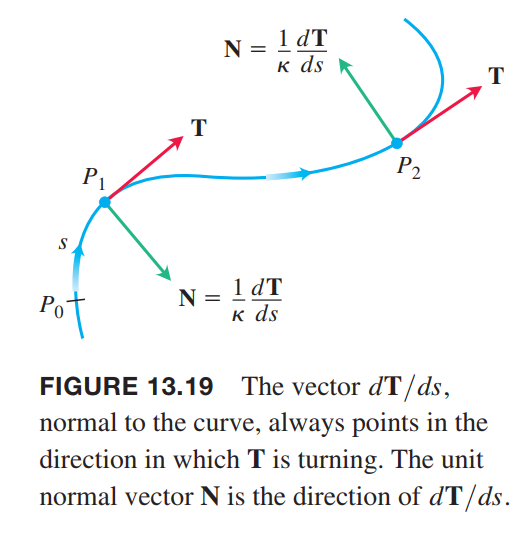
The rate at which $T$ turns per unit of length along the curve is called the curvature (Figure 13.17).
DEFINITION
If $T$ is the unit vector of a smooth curve, the curvature function of the curve is
$$
\kappa = |\frac{dT}{ds}|
$$
If $|dT/ds|$ is large, $T$ turns sharply as the particle passes through $P$, and the curvature
at $P$ is large. According to Chain Rule:
$$
\kappa = |\frac{dT}{ds}| = |\frac{dT}{ds}\frac{dt}{ds}| = \frac{1}{|ds/dt|}|\frac{dT}{dt}| = \frac{1}{|\vec{v}|}|\frac{dT}{dt}|
$$
Formula for Calculating Curvature
If $\vec{r(t)}$ is a smooth curve, then the curvature is the scalar function
$$
\kappa = \frac{1}{|\vec{v}|}|\frac{dT}{dt}|
\tag{}
$$
where T = v> 0 v 0 is the unit tangent vector.
Circle of Curvature for Plane Curves
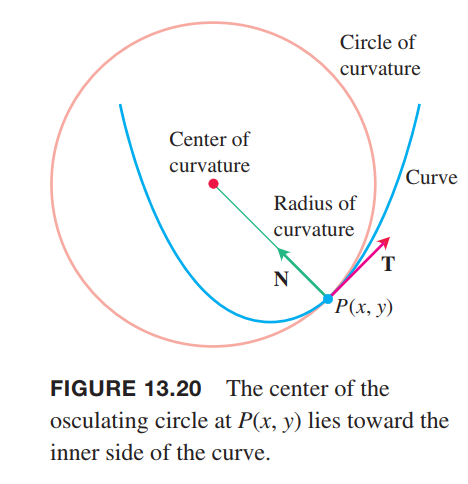
Curvature and Normal Vectors for Space Curves