Keywords: Continuity, The Intermediate Value Theorem
This is the Chapter2 ReadingNotes from book Thomas Calculus 14th.
Continuity
Continuity at a Point
DEFINITIONS
Let $c$ be a real number that is either an interior point or an endpoint of an interval in the domain of $ƒ$.
The function $ƒ$ is continuous at c $if$
$$
\lim_{x\rightarrow c} f(x) = f(c)
$$
The function $ƒ$ is right-continuous at $c$ (or continuous from the right) if
$$
\lim_{x\rightarrow c^+} f(x) = f(c)
$$
The function $ƒ$ is** left-continuous** at c (or continuous from the left) if
$$
\lim_{x\rightarrow c^-} f(x) = f(c)
$$
Continuous Functions
Inverse Functions and Continuity
Continuity of Compositions of Functions
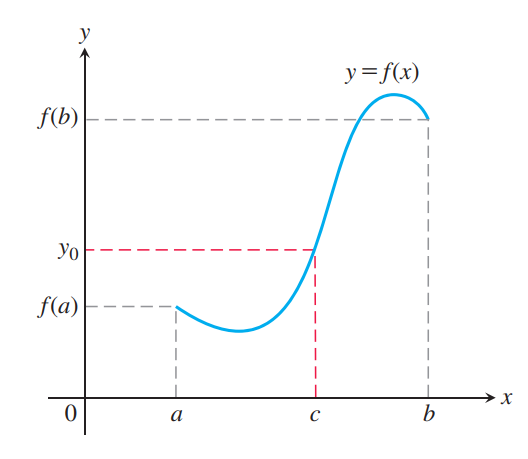
Intermediate Value Theorem for Continuous Functions
THEOREM 11—The Intermediate Value Theorem for Continuous Functions
If $ƒ$ is a continuous function on a closed interval $[a,b]$, and if $y_0$ is any value between $ƒ(a)$ and $ƒ(b)$, then $y_0 = ƒ(c)$ for some $c$ in $[a,b]$.