Keywords: Derivative, Differentiation, ChainRule, Linearization and Differentials
This is the Chapter3 ReadingNotes from book Thomas Calculus 14th.
The Derivative as a Function
Definition
The derivative of the function $f(x)$ with respect to the variable $x$ is the function $f’$ whose value at $x$ is
$$
\begin{aligned}
f’(x) &= \lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}\\
&= \lim_{z\rightarrow x}\frac{f(z)-f(x)}{z-x}
\end{aligned}
$$
If $f’$ exists at a particular $x$, we say that $ƒ$ is differentiable (可微)(has a derivative(有导数)) at $x$. If $f’$ exists at every point in the domain of $f$, we call $f$ differentiable.
The process of calculating a derivative is called differentiation.(求导的过程叫做微分)
$$
f’(x) = \frac{d}{dx}f(x)
$$
Differentiable Functions Are Continuous
If $f$ has a derivative at $x = c$, then $ƒ$ is continuous at $x = c$.
Differentiation Rules
Products and Quotients
Derivative Product Rule
If $u$ and $v$ are differentiable at $x$, then so is their product $uv$, and
$$
\frac{d}{dx}(uv) = u\frac{dv}{dx} + v\frac{du}{dx}
$$
The Chaine Rule
If $ƒ(u)$ is differentiable at the point $u = g(x)$ and $g(x)$ is differentiable at $x$, then the composite function $(ƒ \circ g) (x) = ƒ(g(x))$ is differentiable at x, and
$$
(f\circ g)’(x) = f’(g(x)) \cdot g’(x)
$$
In Leibniz’s notation, if $y = ƒ(u)$ and $u = g(x)$, then
$$
\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}
$$
Implicit Differentiation
$$
\begin{aligned}
&x^3 + y^3 -9xy = 0\\
&y^2-x=0\\
&x^2 + y^2 - 25 = 0
\end{aligned}
$$
These equations define an implicit relation between the variables $x$ and $y$, meaning that a value of $x$ determines one or more values of $y$, even though we do not have a simple formula for the $y$-values.
Implicitly Defined Functions
- Differentiate both sides of the equation with respect to $x$, treating $y$ as a differentiable function of $x$.
- Collect the terms with $\frac{dy}{dx}$ on one side of the equation and solve for $\frac{dy}{dx}$.
Derivatives of Higher Order
Lenses, Tangent Lines, and Normal Lines
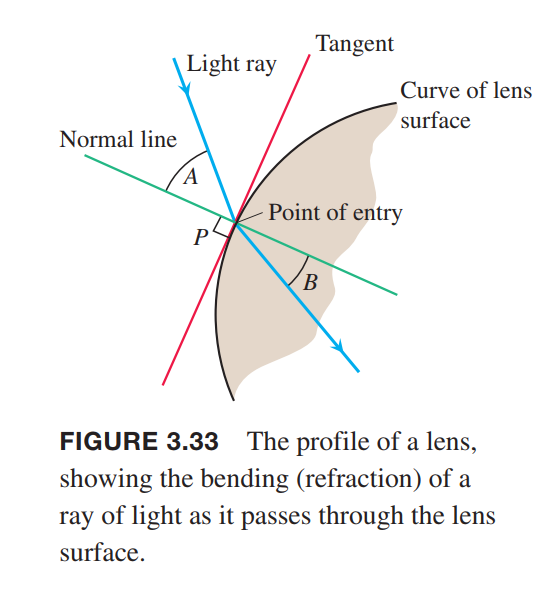
💡For example💡:
Show that the point $(2, 4)$ lies on the curve $x^3 + y^3 - 9xy = 0$. Then find the tangent and normal to the curve there (Figure 3.34).
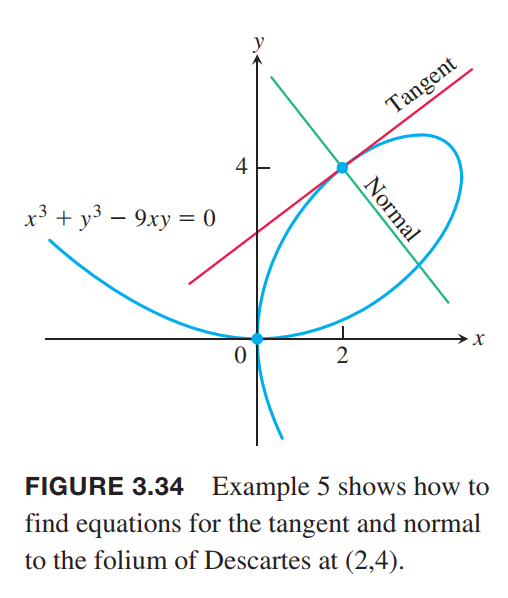
Solution:
To find the slope of the curve at $(2, 4)$, we first use implicit differentiation to find a formula for $\frac{dy}{dx}$:
$$
\begin{aligned}
&x^3 + y^3 -9xy = 0\\
&\frac{d}{dx}(x^3) - \frac{d}{dx}(y^3) - \frac{d}{dx}(9xy) = \frac{d}{dx}(0)\\
&\frac{dy}{dx} = \frac{3y-x^2}{y^2-3x}
\end{aligned}
$$
We then evaluate the derivative at $(x, y) = (2, 4)$:
$$
\left. \frac{dy}{dx}\right|_{(2,4)} = \frac{4}{5}
$$
The tangent at $(2, 4)$ is the line through $(2, 4)$ with slope $\frac{4}{5}$:
$$
y = 4 + \frac{4}{5}(x-2)
$$
The normal line:
$$
y = 4 - \frac{5}{4}(x-2)
$$
Derivatives of Inverse Functions and Logarithms
Derivatives of Inverses of Differentiable Functions
If $ƒ$ has an interval $I$ as domain and $ƒ’(x)$ exists and is never zero on $I$, then $ƒ^{-1}$ is differentiable at every point in its domain (the range of $ƒ$). The value of $(ƒ^{-1})’$ at a point $b$ in the domain of $ƒ^{-1}$ is the reciprocal of the value of $f’$ at the point $a = ƒ^{-1}(b)$:
$$
(f^{-1})’(b) = \frac{1}{f’(f^{-1}(b))}
$$
or
$$
\left. \frac{df^{-1}}{dx}\right|_{x=b} =
$$
$$
\frac{1}{\left. \frac{df}{dx}\right|_{x=f^{-1}(b)}}
$$
Linearization and Differentials(线性化和微分)
It is often useful to approximate complicated functions with simpler ones that give the accuracy we want for specific applications and at the same time are easier to work with than the original functions. The approximating functions discussed in this section are called linearizations, and they are based on tangent lines. Other approximating functions, such as polynomials, are discussed in Chapter 10.
We introduce new variables $dx$ and $dy$, called differentials, and define them in a way that makes Leibniz’s notation for the derivative $\frac{dy}{dx}$ a true ratio.
Linearization
Definition
If $ƒ$ is differentiable at $x = a$, then the approximating function
$$
L(x) = ƒ(a) + ƒ’(a)(x - a)
$$
is the linearization of $ƒ$ at $a$. The approximation
$$
f(x) \approx L(x)
$$
of $ƒ$ by $L$ is the standard linear approximation of $ƒ$ at $a$. The point $x = a$ is the center of the approximation.
Differentials
Definition
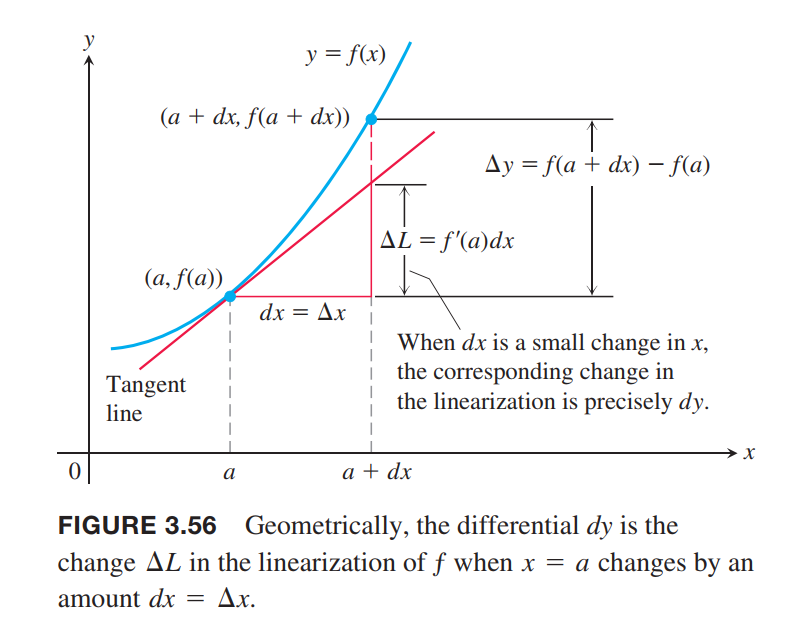
Let $y = ƒ(x)$ be a differentiable function. The differential $dx$ is an independent variable. The differential $dy$ is
$$
dy = f’(x)dx
$$
Estimating with Differentials
💡For example💡:
Use differentials to estimate $\sin(\pi/6+0.01)$.
Solution:
The dierential associated with $y = \sin x$ is
$$
dy = \cos x dx
$$
To estimate $\sin(\pi/6+0.01)$, we set $a = \pi/6$ and $dx = 0.01$. Then
$$
\begin{aligned}
f(\pi/6+0.01) &= f(a + dx) \\
&\approx f(a) + dy\\
&= \sin\frac{\pi}{6} + (\cos\frac{\pi}{6})(0.01)\\
&\approx 0.5087
\end{aligned}
$$
For comparison, the true value of $\sin(\pi/6+0.01)$ to $6$ decimals is $0.508635$.
The method in this example can be used in computer algorithms to give values of trigonometric functions. The algorithms store a large table of sine and cosine values between $0$ and $\pi/4$. Values between these stored values are computed using differentials as in Example. Values outside of $[0,\pi/4]$ are computed from values in this interval using trigonometric identities.
Error in Differential Approximation
Let $ƒ(x)$ be differentiable at $x = a$ and suppose that $dx = \Delta x$ is an increment of $x$. We have two ways to describe the change in $ƒ$ as $x$ changes from $a$ to $a + \Delta x$:
the true change:
$$
\Delta f = f(a + \Delta x) - f(a)
$$
the differential estimate:
$$
df = f’(a)\Delta x
$$
Change in $y = ƒ(x)$ near $x = a$
If $y = ƒ(x)$ is differentiable at $x = a$ and $x$ changes from $a$ to $a + \Delta x$, the change $\Delta y$ in $ƒ$ is given by
$$
\Delta y = f’(a)\Delta x + \epsilon \Delta x
$$
in which $\epsilon \rightarrow 0$ as $\Delta x \rightarrow 0$.
To be added…

