Keywords: Applied Optimization, Concavity and Curve Sketching, Newton’s Method, The Mean Value Theorem
This is the Chapter4 ReadingNotes from book Thomas Calculus 14th.
Extreme Values of Functions on Closed Intervals
DEFINITIONS
Let $ƒ$ be a function with domain $D$. Then $ƒ$ has an absolute maximum value on $D$ at a point $c$ if
$$
f(x) \leq f(c), for \space x \space in \space D
$$
and an absolute minimum value on $D$ at $c$ if
$$
f(x) \geq f(c), for \space x \space in \space D
$$
Maximum and minimum values are called extreme values of the function $ƒ$. Absolute maxima or minima are also referred to as global maxima or minima.
THEOREM 1—The Extreme Value Theorem
If $ƒ$ is continuous on a closed interval $[a,b]$, then $ƒ$ attains both an absolute maximum value $M$ and an absolute minimum value $m$ in $[a,b]$. That is, there are numbers $x_1$ and $x_2$ in $[a,b]$ with $ƒ(x_1) = m, ƒ(x_2) = M$, and $m \leq ƒ(x) \leq M$ for every other $x$ in $[a,b]$.
Local (Relative) Extreme Values
DEFINITIONS
A function $ƒ$ has a local maximum value at a point $c$ within its domain $D$ if $ƒ(x) \leq ƒ(c)$ for all $x \in D$ lying in some open interval containing $c$.
A function $ƒ$ has a local minimum value at a point $c$ within its domain $D$ if $ƒ(x) \geq ƒ(c)$ for all $x \in D$ lying in some open interval containing $c$.
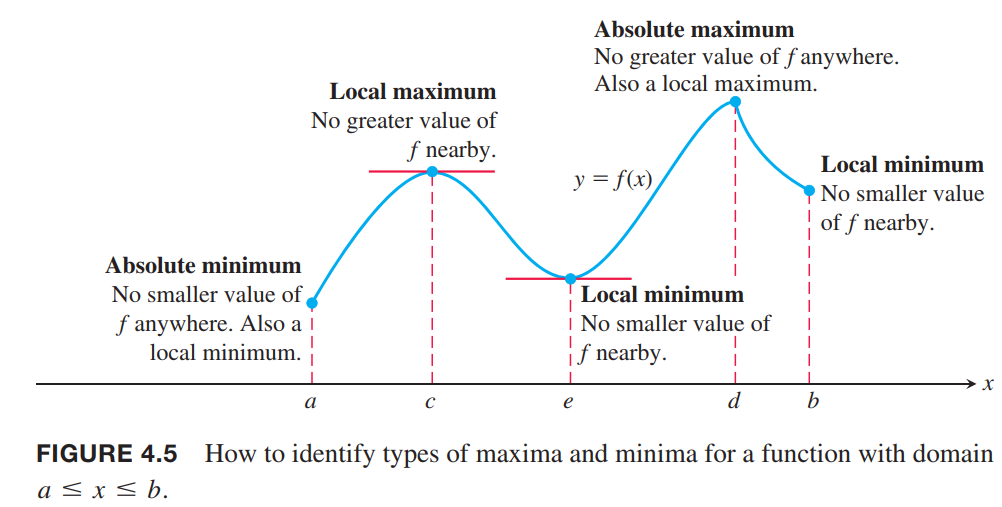
Finding Extrema
THEOREM 2—The First Derivative Theorem for Local Extreme Values
If $ƒ$ has a local maximum or minimum value at an interior point $c$ of its domain, and if $ƒ’$ is defined at $c$, then
$$
f’(c) = 0
$$
DEFINITION
An interior point of the domain of a function $ƒ$ where $ƒ’$ is zero or undefined is a critical point(临界点) of $ƒ$.
The Mean Value Theorem
Rolle’s Theorem(罗尔定理)
THEOREM 3—Rolle’s Theorem
Suppose that $y = ƒ(x)$ is continuous over the closed interval $[a,b]$ and di£erentiable at every point of its interior $(a, b)$. If $ƒ(a) = ƒ(b)$, then there is at least one number $c$ in $(a, b)$ at which $ƒ’(c) = 0$.
The Mean Value Theorem(中值定理)
THEOREM 4—The Mean Value Theorem
Suppose $y = ƒ(x)$ is continuous over a closed interval $[a,b]$ and differentiable on the interval’s interior $(a, b)$. Then there is at least one point $c$ in $(a, b)$ at which
$$
\frac{f(b) - f(a)}{b-a} = f’(c)
$$
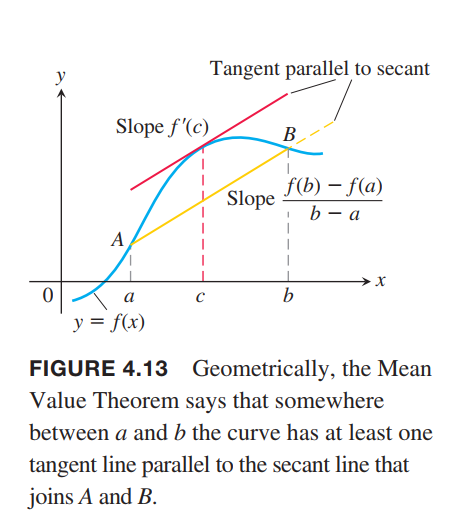
A Physical Interpretation
We can think of the number $\frac{f(b) - f(a)}{b-a}$ as the average change in $ƒ$ over $[a,b]$ and $ƒ’(c)$ as an instantaneous change. Then the Mean Value Theorem says that the instantaneous change at some interior point is equal to the average change over the entire interval.
Finding Velocity and Position from Acceleration
Monotonic Functions and the First Derivative Test
Increasing Functions and Decreasing Functions
COROLLARY 3
Suppose that $ƒ$ is continuous on $[a,b]$ and di£erentiable on $(a, b)$.
If $ƒ’(x) > 0$ at each point x \in (a, b), then $ƒ$ is increasing on $[a,b]$.
If $ƒ’(x) < 0$ at each point $x \in (a, b)$, then $ƒ$ is decreasing on $[a,b]$.
First Derivative Test for Local Extrema
First Derivative Test for Local Extrema
Suppose that $c$ is a critical point of a continuous function $ƒ$, and that $ƒ$ is differentiable at every point in some interval containing $c$ except possibly at $c$ itself. Moving across this interval from left to right,
- if ƒ’ changes from negative to positive at $c$, then $ƒ$ has a local minimum at $c$;
- if $ƒ’$ changes from positive to negative at $c$, then $ƒ$ has a local maximum at $c$;
- if $ƒ’$ does not change sign at $c$ (that is, ƒ’ is positive on both sides of $c$ or negative on both sides), then $ƒ$ has no local extremum at $c$.
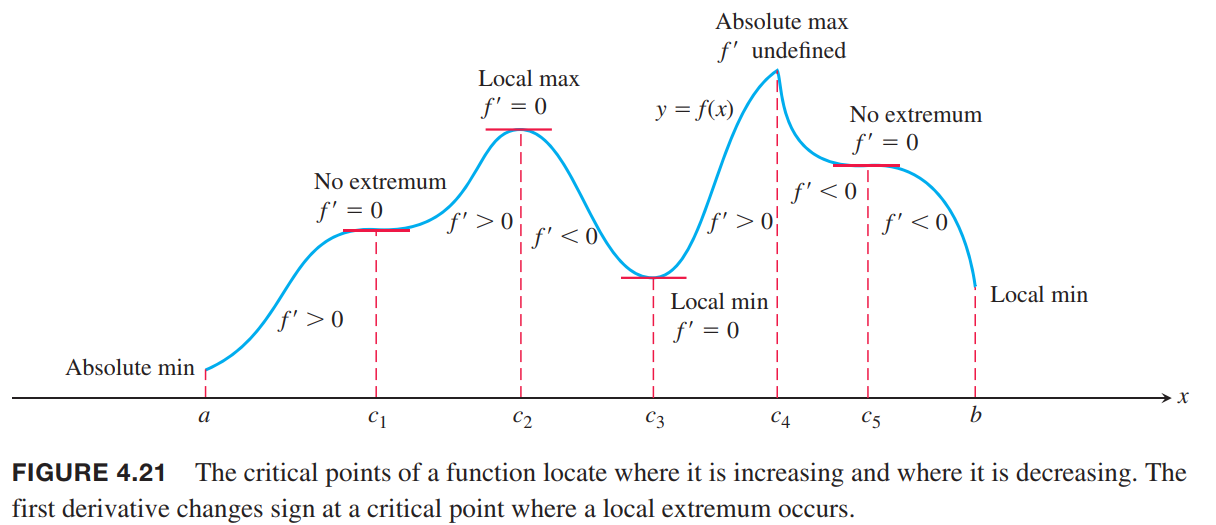
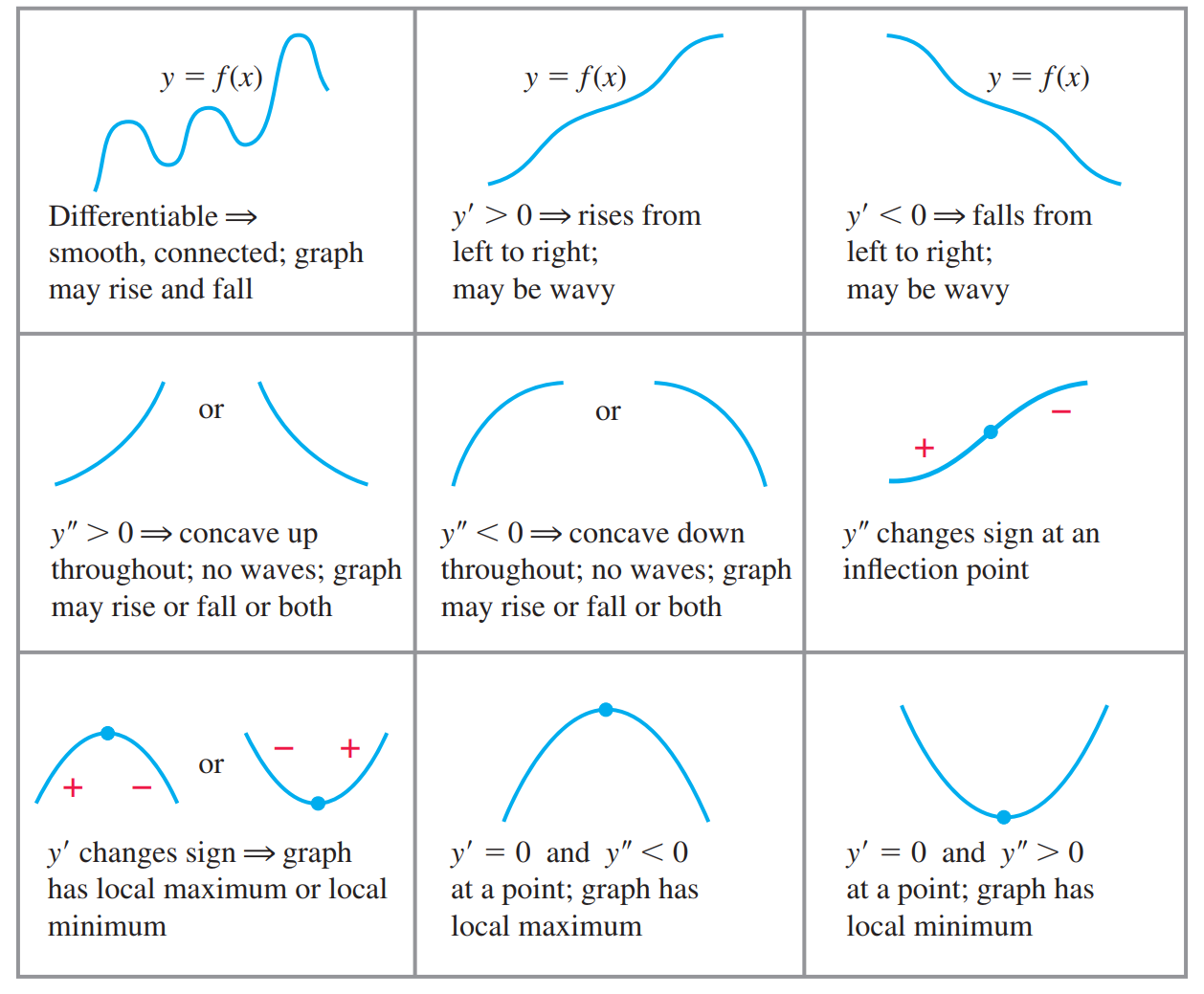
Concavity and Curve Sketching
Concavity
DEFINITION
The graph of a differentiable function $y = ƒ(x)$ is
(a) concave up on an open interval $I$ if $ƒ’$ is increasing on $I$;
(b) concave down on an open interval $I$ if $ƒ’$ is decreasing on $I$.
A function whose graph is concave up is also often called convex.
The Second Derivative Test for Concavity
Let $y = ƒ(x)$ be twice-di£erentiable on an interval $I$.
- If $ƒ’’> 0$ on $I$, the graph of $ƒ$ over $I$ is concave up.
- If $ƒ’’ < 0$ on $I$, the graph of $ƒ$ over $I$ is concave down.
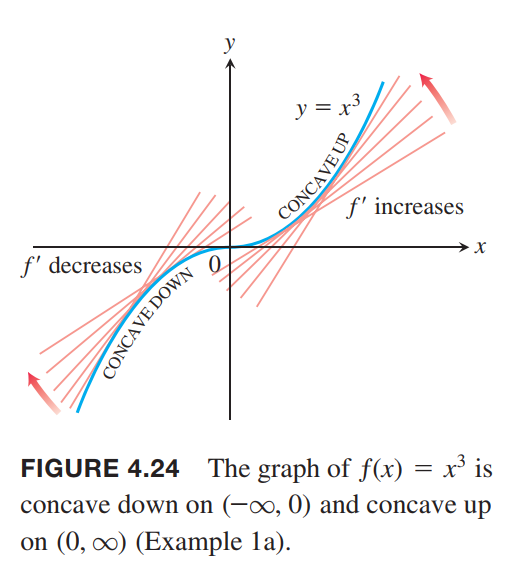
Points of Inflection
DEFINITION
A point $(c, ƒ(c))$ where the graph of a function has a tangent line and where the concavity changes is a point of inflection(拐点).
At a point of inflection $(c, ƒ(c))$, either $ƒ’’(c) = 0$ or $ƒ’’(c)$ fails to exist.
Second Derivative Test for Local Extrema
THEOREM 5—Second Derivative Test for Local Extrema
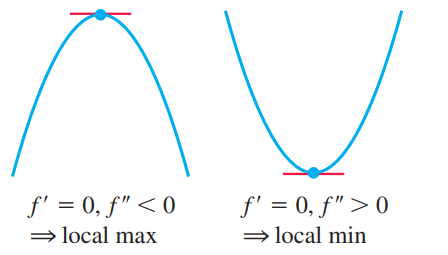
- If $ƒ’(c) = 0$ and $ƒ’’(c) < 0$, then $ƒ$ has a local maximum at $x = c$.
- If $ƒ’(c) = 0$ and ƒ’’(c) > 0, then $ƒ$ has a local minimum at $x = c$.
- If $ƒ’(c) = 0$ and $ƒ’’(c) = 0$, then the test fails. The function $ƒ$ may have a local maximum, a local minimum, or neither.
The following figure summarizes how the first derivative and second derivative affect the shape of a graph.
Indeterminate Forms and L’Hôpital’s Rule(洛必达法则)
Indeterminate Form 0/0
THEOREM 6—L’Hôpital’s Rule
Suppose that $ƒ(a) = g(a) = 0$, that $ƒ$ and $g$ are differentiable on an open interval $I$ containing $a$, and that $g’(x) \neq 0$ on $I$ if $x \neq a$. Then
$$
\lim_{x\rightarrow a}\frac{f(x)}{g(x)} = \lim_{x\rightarrow a}\frac{f’(x)}{g’(x)}
$$
Applied Optimization
Solving Applied Optimization Problems
- Read the problem. Read the problem until you understand it. What is given? What is the unknown quantity to be optimized?
- Draw a picture. Label any part that may be important to the problem.
- Introduce variables. List every relation in the picture and in the problem as an equation or algebraic expression, and identify the unknown variable.
- Write an equation for the unknown quantity. If you can, express the unknown as a function of a single variable or in two equations in two unknowns. This may require considerable manipulation.
- Test the critical points and endpoints in the domain of the unknown. Use what you know about the shape of the function’s graph. Use the first and second derivatives to identify and classify the function’s critical points.
Examples from Mathematics and Physics
💡For example💡:
The speed of light depends on the medium through which it travels, and is generally slower in denser media.
Fermat’s principle in optics states that light travels from one point to another along a path for which the time of travel is a minimum. Describe the path that a ray of light will follow in going from a point $A$ in a medium where the speed of light is $c_1$ to a point $B$ in a second medium where its speed is $c_2$.
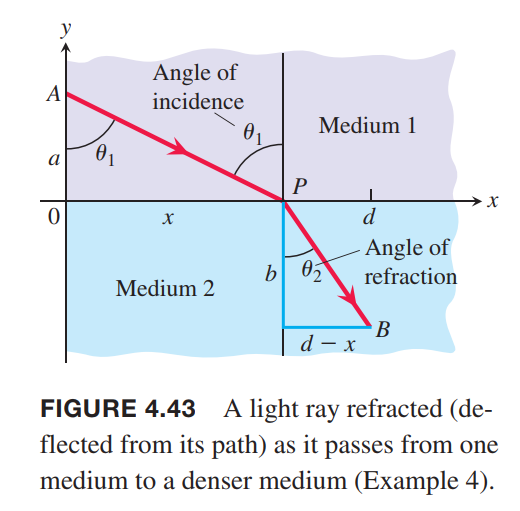
Solution:
$$
t_1 = \frac{AP}{c_1} = \frac{\sqrt{a^2+x^2}}{c_1}\\
t_2 = \frac{PB}{c_2} = \frac{\sqrt{v^2 + (d-x)^2}}{c_2}\\
t = t_1 + t_2
$$
This equation expresses $t$ as a differentiable function of $x$ whose domain is $[0,d]$. We want to find the absolute minimum value of $t$ on this closed interval. We find the derivative
$$
\frac{dt}{dx} = \frac{x}{c_1\sqrt{a^2+x^2}} - \frac{d-x}{c_2\sqrt{b^2+(d-x)^2}}
$$
and observe that it is continuous. In terms of the angles $\theta_1$ and $\theta_2$ in Figure 4.43,
$$
\frac{dt}{dx} = \frac{\sin\theta_1}{c_1} - \frac{\sin\theta_2}{c_2}
$$
The function $t$ has a negative derivative at $x = 0$ and a positive derivative at $x = d$. Since $dt/dx$ is continuous over the interval [0,d], by the Intermediate Value Theorem for continuous functions, there is a point $x \in [0,d]$, where $dt/dx = 0$
$$
\frac{\sin\theta_1}{c_1} = \frac{\sin\theta_2}{c_2}
$$
This equation is Snell’s Law or the Law of Refraction,
Newton’s Method
Procedure for Newton’s Method
Applying Newton’s Method
The goal of Newton’s method for estimating a solution of an equation $ƒ(x) = 0$ is to produce a sequence of approximations that approach the solution.
Newton’s Method
- Guess a first approximation to a solution of the equation $ƒ(x) = 0$. A graph of $y = ƒ(x)$ may help.
- Use the first approximation to get a second, the second to get a third, and so on, using the formula
$$
x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)}, if f’(x_n) \neq 0.
$$
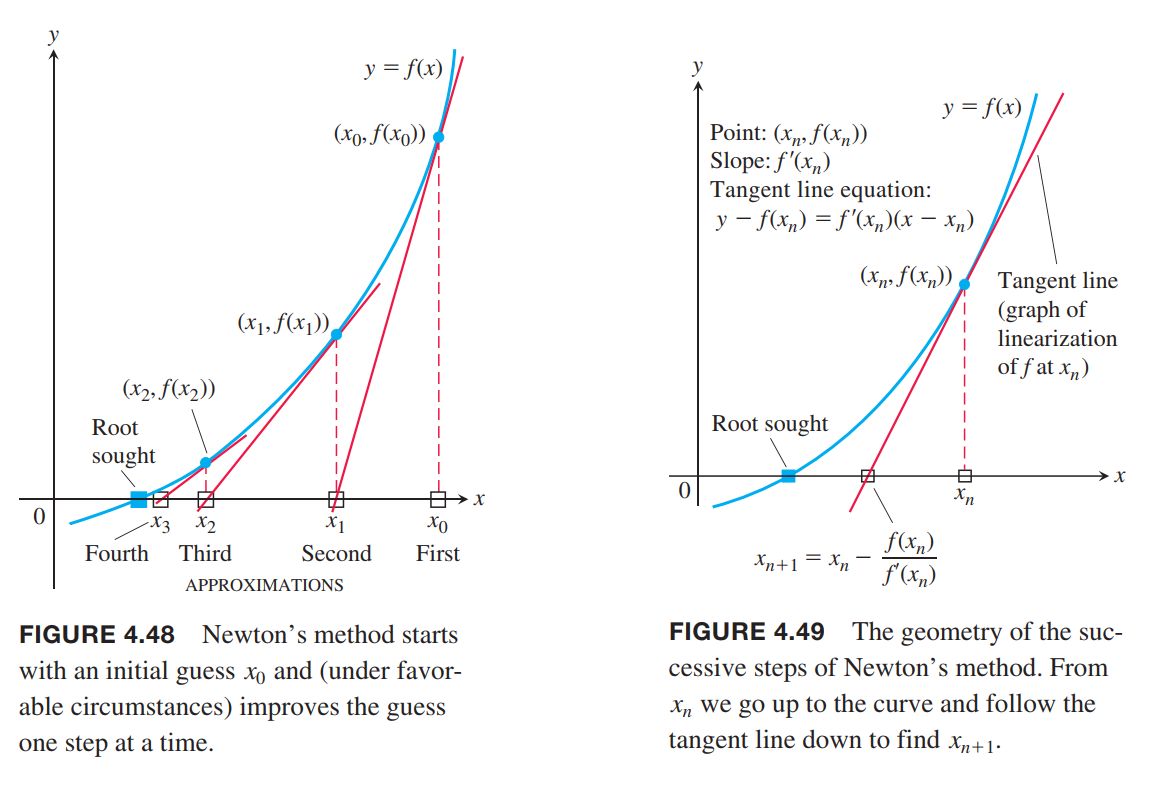
Convergence of the Approximations
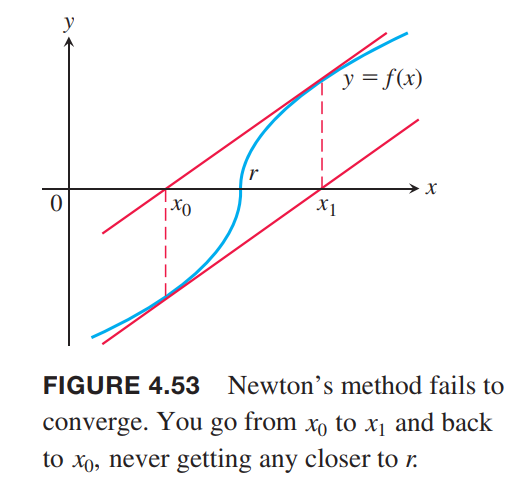
In practice, Newton’s method usually gives convergence with impressive speed, but this is not guaranteed.
One way to test convergence is to begin by graphing the function to estimate a good starting value for $x_0$. You can test that you are getting closer to a zero of the function by checking that $|ƒ(x_n)|$ is approaching zero, and you can check that the approximations are converging by evaluating $|x_n - x_{n+1}|$.
Newton’s method does not always converge. For instance, if
$$
f(x) =
\begin{cases}
-\sqrt{r-x}, x < r\\
\sqrt{x-r}, x \geq r
\end{cases}
$$
there are other fails:
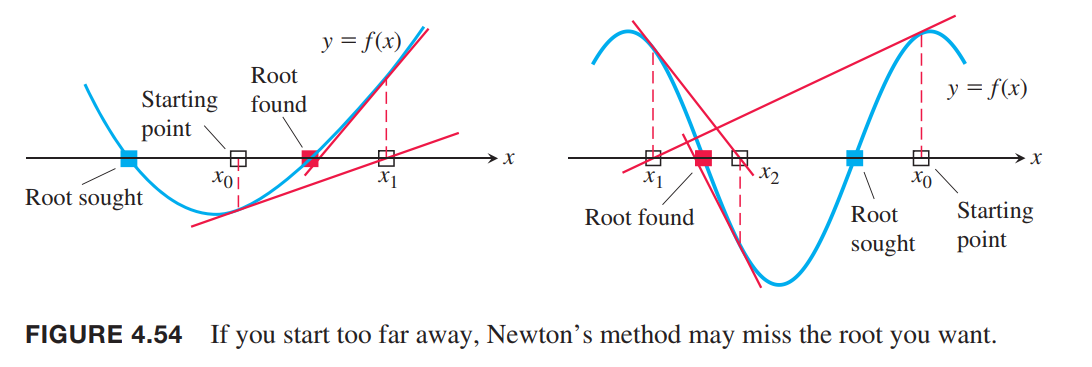
To be added…

