Keywords: Riemann Sums, Mean Value Theorem
This is the Chapter5 ReadingNotes from book Thomas Calculus 14th.
Sigma Notation and Limits of Finite Sums
Riemann Sums
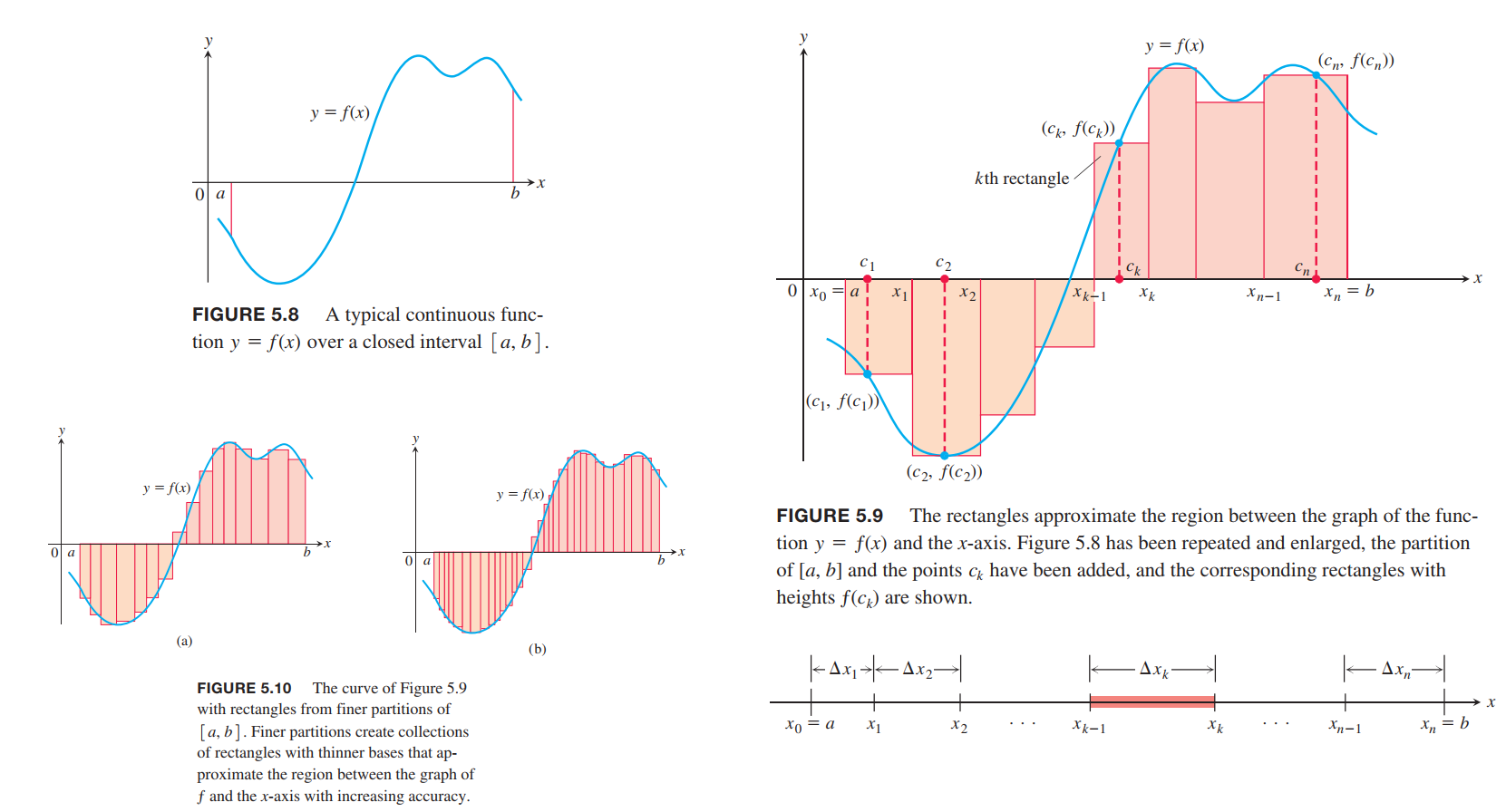
The set of all of these points,
$$
P = \lbrace x_0, x_1, \cdots, x_n \rbrace
$$
is called a partition $P$ of $[a,b]$.
$$
S_p = \sum_{k=1}^n f(c_k)\Delta x_k
$$
The sum $S_P$ is called a Riemann sum for $ƒ$ on the interval $[a,b]$.
we could choose $n$ subintervals all having equal width $\Delta x = (b-a) / n$ to partition $[a,b]$, and then choose the point $c_k$ to be the right-hand endpoint of each subinterval when forming the Riemann sum. This choice leads to the Riemann sum formula
$$
S_n = \sum_{k=1}^n f(a + k\frac{(b-a)}{n}) \cdot (\frac{b-a}{n})
$$
We define the norm(范数) of a partition $P$, written $||P||$, to be the largest of all the subinterval widths. If $||P||$ is a small number, then all of the subintervals in the partition $P$ have a small width.
范数(norm)是数学中的一种基本概念。在泛函分析中,它定义在赋范线性空间中,并满足一定的条件,即①非负性;②齐次性;③三角不等式。它常常被用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。
The Definite Integral
Definition of the Definite Integral
DEFINITION
Let $ƒ(x)$ be a function defined on a closed interval [a,b]. We say that a number $J$ is the definite integral of $ƒ$ over $[a,b]$ and that $J$ is the limit of the Riemann sums $\sum_{k=1}^n f(c_k)\Delta x_k$ if the following condition is satisfied:
Given any number $\epsilon < 0$ there is a corresponding number $\delta > 0$ such that for every partition $P = \lbrace x_0, x_1, \cdots, x_n\rbrace$ of $[a,b]$ with $||P|| < \delta$ and any choice of $c_k$ in $[x_{k-1},x_k]$, we have
$$
|\sum_{k=1}^{n}f(c_k)\Delta x_k - J| < \epsilon
$$
where, $J = \lim_{||P||->0} \sum_{k=1}^{n}f(c_k)\Delta x_k$
A Formula for the Riemann Sum with Equal-Width Subintervals
$$
\int_a^b f(x) dx = \lim_{n->\infty} \sum_{k=1}^n f(a + k \frac{b-a}{n})(\frac{b-a}{n})
\tag{1}
$$
Integrable and Nonintegrable Functions
THEOREM 1—Integrability of Continuous Functions
If a function $ƒ$ is continuous over the interval $[a,b]$, or if $ƒ$ has at most finitely many jump discontinuities there, then the definite integral $\int_a^b f(x)dx$ exists and $ƒ$ is integrable over $[a,b]$.
Properties of Definite Integrals
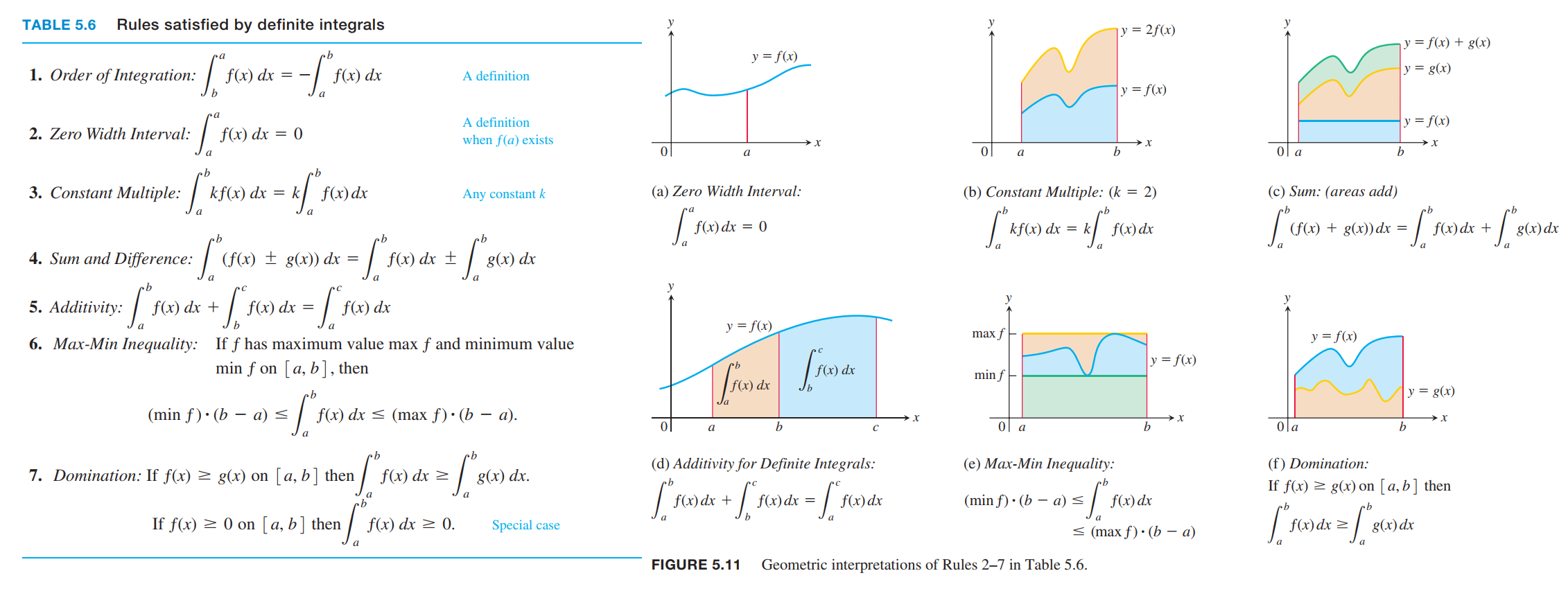
Area Under the Graph of a Nonnegative Function
Theorem 1 guarantees that all of these Riemann sums converge to a single definite integral as the norm of the partitions approaches zero and the number of subintervals goes to infinity.
DEFINITION
If $y = ƒ(x)$ is nonnegative and integrable over a closed interval $[a, b]$, then the area under the curve $y = ƒ(x)$ over $[a,b]$ is the integral of $ƒ$ from $a$ to $b$,
$$
A = \int_a^b f(x)dx
$$
Average Value of a Continuous Function Revisited
DEFINITION
If ƒ is integrable on $[a,b]$, then its average value on $[a,b]$, which is also called its mean, is
$$
av(f) = \frac{1}{b-a}\int_a^b f(x)dx
$$
The Fundamental Theorem of Calculus
Fundamental Theorem of Calculus, which is the central theorem of integral calculus. It connects integration and differentiation, enabling us to compute integrals by using an antiderivative of the integrand function rather than by taking limits of Riemann sums.
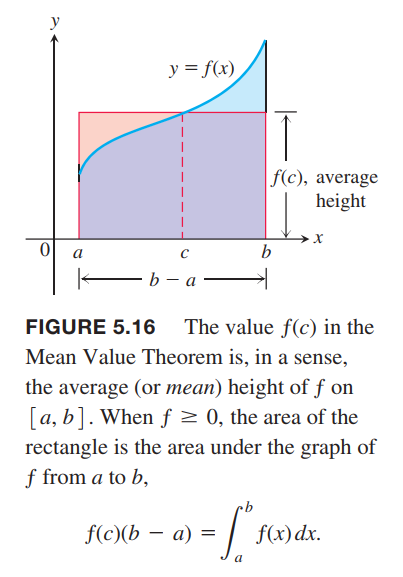
Mean Value Theorem for Definite Integrals(定积分的中值定理)
THEOREM 3—The Mean Value Theorem for Definite Integrals
If $ƒ$ is continuous on $[a,b]$, then at some point $c$ in [a,b],
$$
f(c) = \frac{1}{b-a}\int_a^b f(x) dx
$$
Fundamental Theorem, Part 1
If $ƒ(t)$ is an integrable function over a finite interval $I$, then the integral from any fixed number $a \in I$ to another number $x \in I$ defines a new function $F$ whose value at $x$ is
$$
F(x) = \int_a^xf(t)dt
\tag{1}
$$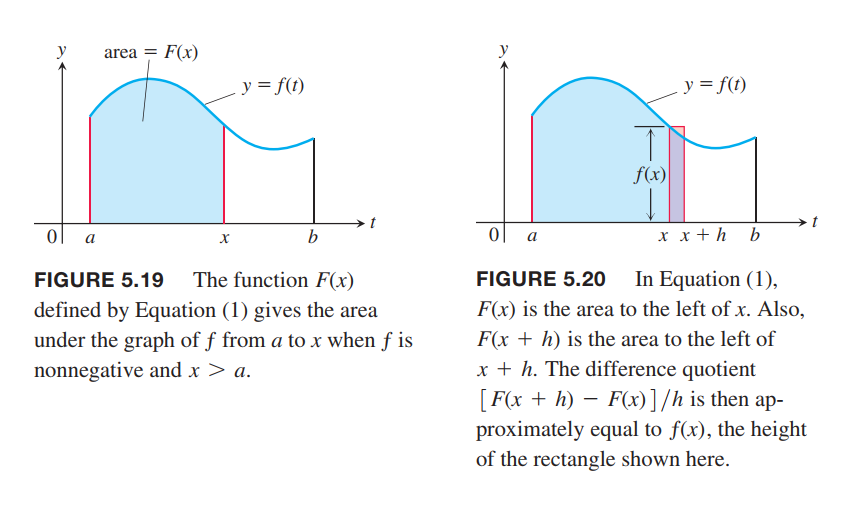
It is reasonable to expect that $F’(x)$, which is the limit of this difference quotient as $h\rightarrow 0$, equals ƒ(x), so that
$$
F’(x) = \lim_{h\rightarrow 0} \frac{F(x+h) - F(x)}{h} = f(x)
$$
THEOREM 4—The Fundamental Theorem of Calculus, Part 1
If $ƒ$ is continuous on [a,b], then $F(x) = \int_a^x ƒ(t) dt$ is continuous on $[a,b]$ and differentiable on $(a,b)$ and its derivative is $ƒ(x)$:
$$
F’(x) = \frac{d}{dx}\int_a^xf(t)dt = f(x)
\tag{2}
$$
Fundamental Theorem, Part 2 (The Evaluation Theorem)
THEOREM 4 (Continued)—The Fundamental Theorem of Calculus, Part 2
If $ƒ$ is continuous over [a,b], and $F$ is any antiderivative of $ƒ$ on [a,b], then
$$
\int_a^b f(x)dx = F(b) - F(a)
$$
The Integral of a Rate
THEOREM 5—The Net Change Theorem
The net change in a differentiable function $F(x)$ over an interval $a \leq x \leq b$ is the integral of its rate of change:
$$
F(b) - F(a) = \int_a^bF’(x)dx
\tag{6}
$$
The Relationship Between Integration and Differentiation
The conclusions of the Fundamental Theorem tell us several things. Equation (2) can be rewritten as
$$
\frac{d}{dx}\int_a^xf(t)dt = f(x)
$$
which says that if you first integrate the function $ƒ$ and then differentiate the result, you get the function $ƒ$ back again.
Likewise, replacing $b$ by $x$ and $x$ by $t$ in Equation (6) gives
$$
\int_a^x F’(t)dt = F(x)-F(a)
$$
so that if you first differentiate the function $F$ and then integrate the result, you get the function $F$ back (adjusted by an integration constant).
In a sense, the processes of integration and differentiation are “inverses” of each other.
Indefinite Integrals and the Substitution Method
The connection between antiderivatives and the definite integral stated in the Fundamental Theorem now explains this notation:
$$
\begin{aligned}
\int_a^b f(x)dx &= F(b) - F(a) \\
&= \left[F(b) + C\right] - \left[F(a) + C\right] \\
&= \left[F(x) + C\right]_a^b \\
&= \left[\int f(x) dx\right]_a^b
\end{aligned}
$$
Substitution: Running the Chain Rule Backwards
If $u$ is a differentiable function of $x$, then
$$
du = \frac{du}{dx} dx
$$
THEOREM 6—The Substitution Rule
If $u = g(x)$ is a differentiable function whose range is an interval $I$, and $ƒ$ is continuous on $I$, then
$$
\int f(g(x)) \cdot g’(x)dx = \int f(u) du
$$
Definite Integral Substitutions and the Area Between Curves
The Substitution Formula
THEOREM 7—Substitution in Definite Integrals
If $g’$ is continuous on the interval $[a,b]$ and $ƒ$ is continuous on the range of $g(x) = u$, then
$$
\int_a^b f(g(x))g’(x)dx = \int_{g(a)}^{g(b)} f(u) du
$$
Definite Integrals of Symmetric Functions
THEOREM 8 Let $ƒ$ be continuous on the symmetric interval $[-a,a]$.
a. If $f$ is even, then $\int_{-a}^a f(x) dx = 2\int_0^a f(x)dx$
b. If $f$ is odd, then, $\int_{-a}^a f(x) dx = 0$
Areas Between Curves
DEFINITION
If $ƒ$ and $g$ are continuous with $ƒ(x) \geq g(x)$ throughout $[a,b]$, then the area of the region between the curves $y = f (x)$ and $y = g(x)$ from $a$ to $b$ is the integral of $(ƒ - g)$ from $a$ to $b$:
$$
A = \int_a^b \left[ f(x) - g(x) \right] dx
$$
To be added…

