Keywords: Arc Length, Work and Fluid Forces, Moments and Centers of Mass
This is the Chapter6 ReadingNotes from book Thomas Calculus 14th.
Arc Length
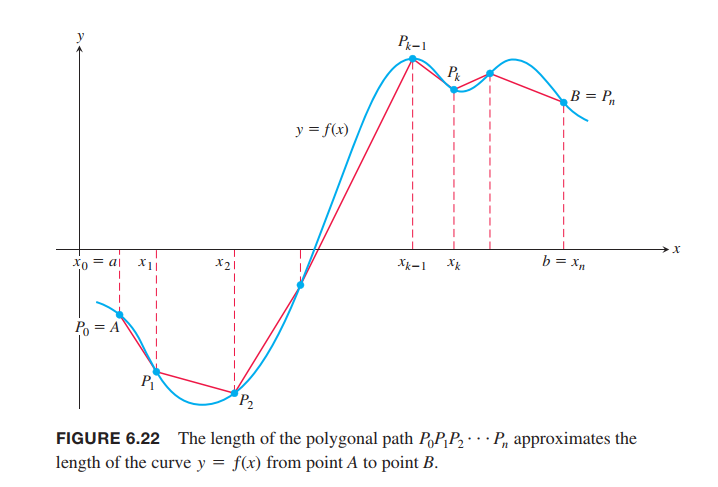
We divide the curve into many pieces, and we approximate each piece by a straight-line segment.The total length of the curve is the limiting value of these approximations as the number of segments goes to infinity.
Length of a Curve $y = ƒ(x)$
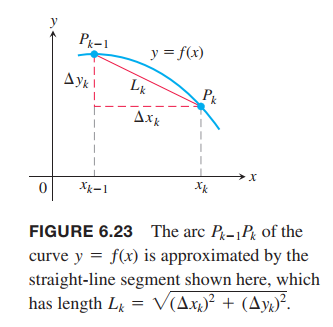
If we set $\Delta x_k = x_k - x_{k-1}$ and $\Delta y_k = y_k - y_{k-1}$, then a representative line segment in the path has length (see Figure 6.23)
$$
L_k = \sqrt{(\Delta x_k)^2 + (\Delta y_k)^2}
$$
so the length of the curve is approximated by the sum
$$
\sum_{k=1}^n L_k = \sum_{k=1}^n \sqrt{(\Delta x_k)^2 + (\Delta y_k)^2}
\tag{1}
$$
In order to evaluate this limit, we use 👉the Mean Value Theorem, which tells us that there is a point $c_k$ , with $x_{k-1} < c_k < x_k$, such that
$$
\Delta y_k = f’(c_k)\Delta x_k
$$
Substituting this for $\Delta y_k$, the sums in Equation (1) take the form
$$
\sum_{k=1}^n L_k = \sum_{k=1}^n \sqrt{(\Delta x_k)^2 + (f’(c_k)\Delta x_k)^2}
=\Delta x_k \sum_{k=1}^n \sqrt{1 + [f’(c_k)]^2}
\tag{2}
$$
This is a 👉Riemann sum whose limit we can evaluate. Because $\sqrt{1 + [f’(c_k)]^2}$ is continuous on $[a,b]$, the limit of the Riemann sum on the right-hand side of Equation (2) exists and has the value
$$
\lim_{n\rightarrow \infty} \sum_{k=1}^n L_k = \lim_{n\rightarrow \infty} \Delta x_k \sum_{k=1}^n \sqrt{1 + [f’(c_k)]^2} =
\int_a^b \sqrt{1 + [f’(x)]^2} dx
$$
DEFINITION
If $ƒ’$ is continuous on $[a,b]$, then the length (arc length) of the curve $y = ƒ(x)$ from the point $A = (a, ƒ(a))$ to the point $B = (b, ƒ(b))$ is the value of the integral
$$
L = \int_a^b \sqrt{1 + [f’(x)]^2} dx = \int_a^b \sqrt{1 + [\frac{dy}{dx}]^2} dx
$$
Work and Fluid Forces
Moments and Centers of Mass
To be added…

