Keywords: Numerical Integration, Simpson’s Rule
This is the Chapter8 ReadingNotes from book Thomas Calculus 14th.
Integration by Parts
Product Rule in Integral Form
If $u$ and $v$ are differentiable functions of $x$, the 👉Product Rule says that
$$
\frac{d}{dx}\left[ u(x)v(x) \right] = u’(x)v(x) + u(x)’v(x)
$$
In terms of indefinite integrals, this equation becomes
$$
\begin{aligned}
\int \frac{d}{dx}\left[ u(x)v(x)\right]dx &= \int \left[u’(x)v(x) + u(x)’v(x)\right]dx \\
&= \int u’(x)v(x) dx + \int u(x)’v(x) dx \\
\Longrightarrow
\int u(x)’v(x) dx &= \int \frac{d}{dx}\left[ u(x)v(x)\right]dx - \int u’(x)v(x) dx
\end{aligned}
$$
Integration by Parts Formula
$$
\int u(x) v’(x) dx = u(x)v(x) - \int v(x)u’(x)dx
\tag{1}
$$
With $v’(x) dx = dv$ and $u’(x) dx = du$, the integration by parts formula becomes
$$
\int udv = uv - \int vdu
$$
Evaluating Definite Integrals by Parts
The integration by parts formula in Equation (1) can be combined with Part 2 of the Fundamental
Theorem in order to evaluate definite integrals by parts. Assuming that both $u’$ and $y’$ are continuous over the interval $[a,b]$, Part 2 of the Fundamental Theorem gives
Integration by Parts Formula for Definite Integrals
$$
\int_a^b u(x)v’(x) dx = \left. u(x)v(x) \right|_z^b - \int_a^b v(x)u’(x)dx
$$
Numerical Integration
When we cannot find a workable antiderivative(不定积分)for a function $ƒ$ that we have to integrate, we can partition the interval of integration, replace $ƒ$ by a closely fitting polynomial on each subinterval, integrate the polynomials, and add the results to approximate the definite integral of $ƒ$. This procedure is an example of numerical integration.
Trapezoidal Approximations(梯形近似)
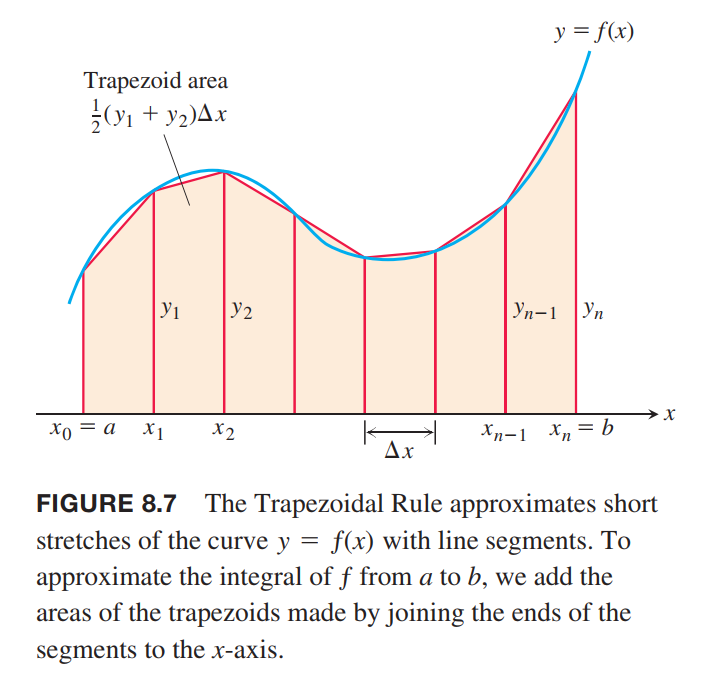
The Trapezoidal Rule
To approximate $\int_a^b f(x) dx$, use
$$
T = \frac{\Delta x}{2}(y_0 + 2y_1 + 2y_2 + \cdots + y_n)
$$
The y’s are the values of $ƒ$ at the partition points
$$
x_0 = a, x_1 = a + \Delta x, x_2 = a + 2 \Delta x, \cdots, x_{n-1} = a + (n-1)\Delta x, x_n = b,
$$
where, $\Delta x = (b-a)/n$
Simpson’s Rule: Approximations Using Parabolas(抛物线近似)
Another rule for approximating the definite integral of a continuous function results from using parabolas instead of the straight-line segments that produced trapezoids.
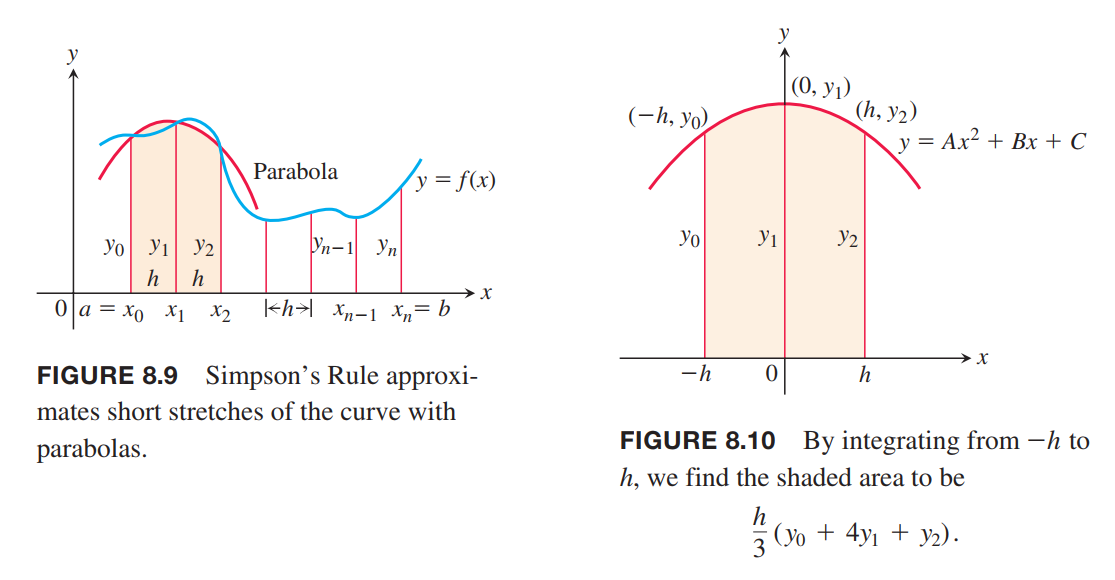
Simpson’s Rule
To approximate $\int_a^b f(x) dx$, use
$$
S = \frac{\Delta x}{3}(y_0 + 4y_1 + 4y_2 + \cdots + 2y_{n-2} + 4y_{n-1} + y_n)
$$
The y’s are the values of $ƒ$ at the partition points
$$
x_0 = a, x_1 = a + \Delta x, x_2 = a + 2 \Delta x, \cdots, x_{n-1} = a + (n-1)\Delta x, x_n = b,
$$
where, $\Delta x = (b-a)/n$
Error Analysis
To be added…

