Keywords: Determinants, Linear Transformation, Area or Volume, Cramer’s Rule
This is the Chapter3 ReadingNotes from book Linear Algebra and its Application.
Introduction to Determinants
If $A$ is a triangular matrix, then det $A$ is the product of the entries on the main diagonal of $A$.
The determinant of an $n \times n$ matrix $A$ can be computed by a cofactor expansion across any row or down any column. The expansion across the $i-th$ row using the cofactors is
$$
\begin{aligned}
det A &= a_{i1}C_{i1} + a_{i2}C_{i2} + \cdots + a_{in}C_{in}\\
C_{ij} &= (-1)^{i+j}detA_{i,j}
\end{aligned}
$$
在计算机中是怎么计算行列式的?
Yet it would be impossible to calculate a $25 \times 25$ determinant by cofactor expansion.
In general, a cofactor expansion requires more than $n!$ multiplications, and $25!$ is approximately $1.5 * 10 ^ {25}$ If a computer performs one trillion multiplications per second, it would have to run for more than $500,000 years$ to compute a $25 \times 25$ determinant by this method. Fortunately, there are faster methods, see the next chapter.
Properties of Deternimants
Let $A$ be a square matrix.
a. If a multiple of one row of $A$ is added to another row to produce a matrix $B$, then $det B = det A$.
b. If two rows of $A$ are interchanged to produce $B$, then $det B = - det A$.
c. If one row of $A$ is multiplied by $k$ to produce $B$, then $det B = k * det A$.
💡For example💡:
Compute $det A$, where $A = \begin{bmatrix}2 & -8 & 6 & 8\\ 3 & -9 & 5 & 10\\ -3 & 0 & 1 & -2\\1 & -4 & 0 & 6\end{bmatrix}$
Solution:
求行列式如下:
$$
det A = 2
\left|
\begin{array}{}
1 & -4 & 3 & 4 \\
3 & -9 & 5 & 10\\
-3 & 0 & 1 & -2\\
1 & -4 & 0 & 6
\end{array}
\right|
=
2
\left|
\begin{array}{}
1 & -4 & 3 & 4 \\
0 & 3 & -4 & -2\\
0 & 0 & -6 & 2\\
0 & 0 & 0 & 1
\end{array}
\right|
=
2\cdot (1)\cdot(3)\cdot(-6)\cdot(1)
= -36
$$
A square matrix $A$ is invertible if and only if $det A \neq$ 0 (因为阶梯式下,对角线上如果有0,矩阵肯定不可逆)
$$
det A = \begin{cases}
(-1)^r \cdot (product\space of \space pivots\space in \space U) & when \space A \space is\space invertible\\
0 & when \space A \space is\space not \space invertible
\end{cases}\tag{1}
\\
U = \begin{bmatrix}
\blacksquare & * & * & * \\
0 & \blacksquare & * & * \\
0 & 0 & \blacksquare & * \\
0 & 0 & 0 & \blacksquare
\end{bmatrix}
$$
$r$: interchange operations in the process of matrix $A \rightarrow U$ .
- Most computer programs that compute $det A$ for a general matrix $A$ use the method of formula (1) above.
- It can be shown that evaluation of an $n \times n$ determinant using row operations requires about $2n^3 / 3$ arithmetic operations. Any modern microcomputer can calculate a $25 \times 25$ determinant in a fraction of a second, since only about $10,000$ operations are required.
Column Operations
If $A$ is an $n \times n$ matrix, then $det A^T = det A$
Determinants and Matrix Products
If $A$ and $B$ are $n \times n$ matrices, then $det AB = detA \cdot detB$.
A Linearity Property of the Determinant Function
$$
A = \begin{bmatrix}
\vec{a_1} & \cdots & \vec{a_{j-1}} & \vec{x}& \vec{a_{j+1}} & \cdots & \vec{a_n}
\end{bmatrix}
\\
T(\vec{x}) = det \begin{bmatrix}
\vec{a_1} & \cdots & \vec{a_{j-1}} & \vec{x}& \vec{a_{j+1}} & \cdots & \vec{a_n}
\end{bmatrix}
\\
T(c\vec{x}) = cT(\vec{x})\\
T(\vec{u}+\vec{v}) = T(\vec{u}) + T(\vec{v})
$$
Cramer’s Rule, Volume, Linear Transformation
Cramer’s Rule(克拉默法则)
Let A be an invertible $n \times n$ matrix. For any $\vec{b}$ in $R^n$, the unique solution $\vec{x}$ of $A\vec{x} = \vec{b}$ has entries given by
$$
\vec{x_i} = \frac{det A_i(\vec{b})}{det A}, i = 1, 2, \cdots, n
$$
$$
det A_i(\vec{b}) =
\begin{bmatrix}
\vec{a_1} & \cdots & \vec{b} & \cdots & \vec{a_n}
\end{bmatrix}
第i列的向量改成了\vec{b}向量
$$
Application to Engineering
Laplace transforms: This approach converts an appropriate system of linear differential equations into a system of linear algebraic equations whose coefficients involve a parameter.(只是提一嘴拉普拉斯变换)
💡For example💡:
Consider the following system in which $s$ is an unspecified parameter. Determine the values of $s$ for which the system has a unique solution, and use Cramer’s rule to describe the solution.
$$
\begin{cases}
3s x_1 - 2x_1 = 4\\
-6x_1 + sx_2 = 1
\end{cases}
$$
Solution:
$$
A = \begin{bmatrix}
3s & -2\\
-6 & s
\end{bmatrix},
A_1(\vec{b}) = \begin{bmatrix}
4 & -2\\
1 & s
\end{bmatrix},
A_2(\vec{b}) = \begin{bmatrix}
3s & 4\\
-6 & 1
\end{bmatrix}
$$
Since,
$$
det A = 3s^2-12 = 3(s+2)(s-2)
$$
so,
$$
unique-solution: s \neq \pm2
\\
x_1 = \frac{det A_1(\vec{b})}{det A} = \frac{4s+2}{3(s+2)(s-2)},
x_1 = \frac{det A_2(\vec{b})}{det A} = \frac{s+8}{(s+2)(s-2)}
$$
A Formula for $A^{–1}$
let $A$ be an invertible $n \times n$ matrix. Then
$$
A^{-1} = \frac{1}{det A} adj A
$$
The adjugate matrix is the transpose of the matrix of cofactors
💡For example💡:
Find the inverse matrix of $A = \begin{bmatrix}2 & 1 & 3\\1 & -1 & 1\\1 & 4 & 2\end{bmatrix}$
Solution:
$$
C_{11} = + \left|
\begin{array}{}
-1 & 1 \\
4 & -2
\end{array}
\right| = -2 , C_{12} = 3, C_{13} = 5,
C_{21} = 14, C_{22} = -7,C_{23} = -7
$$
$$
adj A =
\begin{bmatrix}
-2 & 14 & 4\\
3 & -7 & 1\\
5 & -7 & 3\end{bmatrix}
接下来套公式即可
$$
在计算机中,
For a larger $n \times n$ matrix (real or complex), Cramer’s rule is hopelessly inefficient.
Computing just one determinant takes about as much work as solving $Ax = b$ by row reduction.
Determinants as Area or Volume
If $A$ is a $2 \times 2$ matrix, the area of the parallelogram(平行四边形) determined by the columns of $A$ is $|detA|$.
If $A$ is a $3 \times 3$ matrix, the volume of the parallelepiped(平行六面体) determined by the columns of $A$ is $|detA|$.
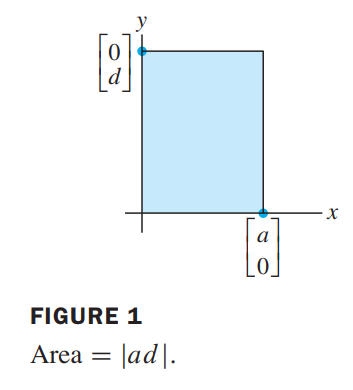
$$
\left|
{}det\begin{bmatrix}a & 0 \\ 0 & d\end{bmatrix}
\right|=
\left|ad\right| = {area \space of \space rectangle}
$$
💡For example💡:
Calculate the area of the parallelogram determined by the points $(-2,-2),(0,3),(4,-1)and (6,4)$
Solution:
求平行四边形面积如下:
$$
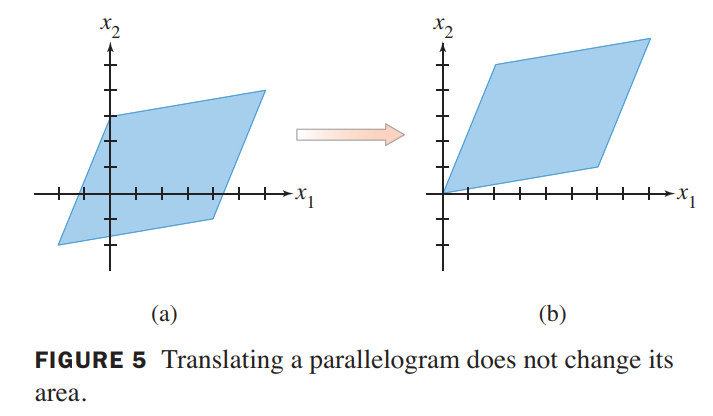
1、平移(如下图),
新点:(0,0), (2,5),(6,1),(8,6)
$$
$$
2、建立矩阵列向量,
A =
\begin{bmatrix}
2 & 5\\
5 & 1
\end{bmatrix},
\left|detA\right| = \left|-28\right|,
面积是28
$$
Linear Transformations
Let $T:R^2\rightarrow R^2$ be the linear transformation determined by a $2 \times 2$ matrix $A$. If $S$ is a parallelogram(or other finite area) in $R^2$, then
$$
(area-of-T(S)) = \left|detA\right| \cdot (area-of-S)
$$
If $T$ is determined by a $3 \times 3$ matrix $A$, and if $S$ is a parallelepiped(or other finite volume) in $R^3$, then
$$
(volume-of-T(S)) = \left|detA\right| \cdot (volume-of-S)
$$
💡for example💡:
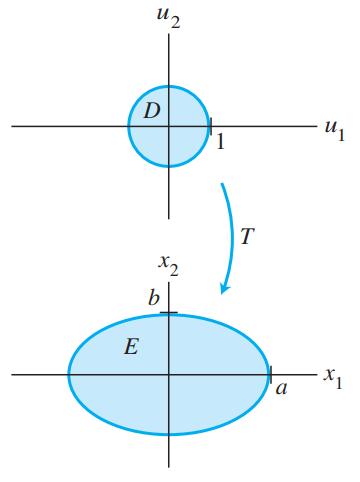
Let $a$ and $b$ be positive numbers. Find the area of the region $E$ bounded by the ellipse whose equation is
$$
\frac{x_1^2}{a^2} + \frac{x_2^2}{b^2} = 1
$$
We claim that $E$ is the image of the unit disk $D$ under the linear transformation $T$ determined by the matrix $A = \begin{bmatrix}a & 0\\ 0 & b\end{bmatrix}$, because if $\vec{u} =\begin{bmatrix}u_1\\u_2\end{bmatrix}$ ,$\vec{x} = \begin{bmatrix}x_1\\x_2\end{bmatrix}$,and $\vec{x} = A\vec{u}$, then
$$
u_1 = \frac{x_1}{a}, u_2 = \frac{x_2}{b}
$$
it follows that $\vec{u}$ is in the unit disk, with $u_1^2 + u_2^2 \leqslant 1$, if and only if $\vec{x}$ is in E, with $(x_1/a)^2 + (x_2/b)^2 \leqslant 1$, so the area of ellipse is :
$$
\begin{aligned}
area \space of \space ellipse &= area \space of \space T(D)\\
&= \left|detA\right| \cdot area \space of \space D\\
&= ab \cdot \pi (1)^2 \\
&= \pi ab
\end{aligned}
$$