Keywords: Numerical Differentiation, Simpson’s Rule, Gaussian Quadrature, Mathlab
Numerical Differentiation(数值微分)
👉More about Differentiation and Derivative in Calculus >>
Finite difference formulas
From 👉Taylor’s Theorem >>, we know if $f$ is twice continuously differentiable, then
$$
f(x+h) = f(x) + hf’(x) + \frac{h^2}{2}f’’(c)
\tag{5.2}
$$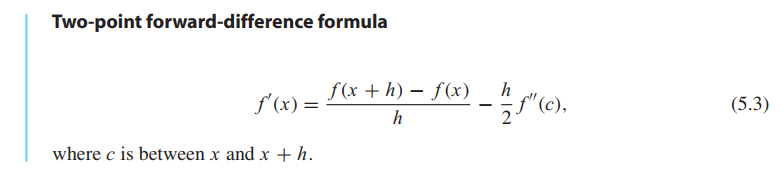
we use the equation (5.3) as the approximation
$$
f’(x) \approx \frac{f(x+h)-f(x)}{h}
\tag{5.4}
$$
and treating the last term in (5.3) as error.
In general, if the error is $O(h^n)$, we call the formula an order $n$ approximation.
Rounding error
Extrapolation
Symbolic differentiation and integration
Newton–Cotes Formulas for Numerical Integration (数值积分)
Trapezoid Rule
Simpson’s Rule
Composite Newton–Cotes formulas
Open Newton–Cotes Methods
Romberg Integration
Adaptive Quadrature
Gaussian Quadrature
Reality Check 5: Motion Control in Computer-Aided Modeling

