NumericalAnalysis-C6-Ordinary-Differential-Equations

Keywords: Euler’s Method, First-order linear equations, Systems of Ordinary Differential Equations, Implicit Methods and Stiff Equations, Mathlab

👉More about First-Order-Differential-Equations in Calculus >>

👉More about Second-Order-Differential-Equations in Calculus >>

Initial Value Problems

A wide majority of interesting equations have no closed-form solution, which leaves approximations as the only recourse.

It will be helpful to think of a differential equation as a field of slopes, When an initial condition is specified on a slope field, one out of the infinite family of solutions can be identified.

Euler’s Method

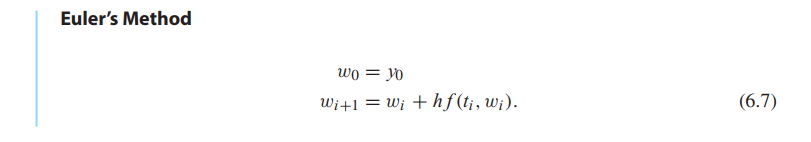
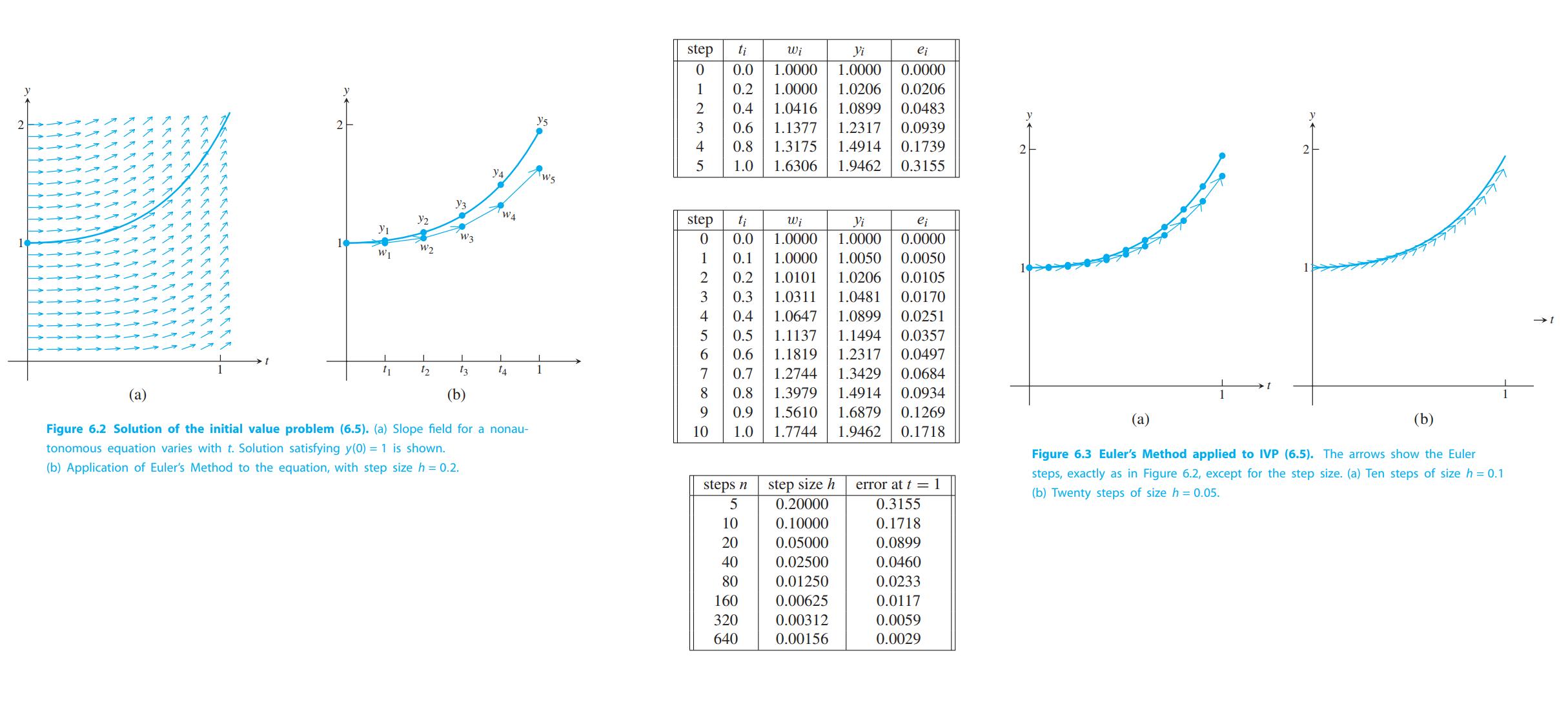
💡For example💡:

draw the slope field of this initial value problem, and apply Euler’s Method to this initial value problem with initial condition $y_0 = 1$
$$
\begin{cases}
y’ = ty + t^3\\
y(0) = y_0\\
t \in [0,1]
\end{cases}
\tag{6.5}
$$

Solution:
The right-hand side of the differential equation is $f(t,y) = ty + t^3$. Therefore, Euler’s Method will be the iteration
$$
w_0 = 1\\
w_{i+1} = w_i + h(t_iw_i + t_i^3)
\tag{6.8}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14

%eulerr.m
%Program 6.1 Euler’s Method for Solving Initial Value Problems
%Use with ydot.m to evaluate rhs of differential equation
% Input: interval inter, initial value y0, number of steps n
% Output: time steps t, solution y
% Example usage: euler([0 1],1,10);
function [t,y]=eulerr(inter,y0,n)
t(1)=inter(1); y(1)=y0;
h=(inter(2)-inter(1))/n;
for i=1:n
    t(i+1)=t(i)+h;
    y(i+1)=eulerstep(t(i),y(i),h);
end
plot(t,y)

1
2
3
4
5
6

%eulerstep.m
function y=eulerstep(t,y,h)
%one step of Euler’s Method
%Input: current time t, current value y, stepsize h
%Output: approximate solution value at time t+h
y=y+h*ydot(t,y);

1
2
3
4

%ydot.m
function z=ydot(t,y)
%right-hand side of differential equation
z=t*y+t^3;

1
2
3
4
5

>> eulerr([0,1],1,10)

ans =

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000

Existence, uniqueness, and continuity for solutions

DEFINITION 6.1
A function $f(t,y)$ is Lipschitz continuous(李普希兹连续) in the variable $y$ on the rectangle $S = [a,b] \times [\alpha,\beta]$ if there exists a constant $L$ (called the Lipschitz constant) satisfying
$$
|f(t,y_1) - f(t,y_2)| \leq L|y_1 - y_2|
$$
for each $(t, y_1), (t ,y_2)$ in $S$.
A function that is Lipschitz continuous in $y$ is continuous in $y$, but not necessarily differentiable.

💡For example💡:

Find the Lipschitz constant for the right-hand side
$$
f(t,y) = ty + t^3
$$
of (6.5).

Solution:

The function $f(t,y) = ty + t^3$ is Lipschitz continuous in the variable $y$ on the set $0 \leq t \leq 1, -\infty < y < +\infty$. Check that
$$
|f(t,y_1) - f(t,y_2)| = |ty_1 - ty_2| \leq |t||y_1-y_2| \leq |y_1 - y_2|
\tag{6.10}
$$
on the set. The Lipschitz constant is $L = 1$.

If the function $f$ is continuously differentiable in the variable $y$, the maximum absolute value of the partial derivative $\frac{\partial f}{\partial y}$ is a Lipschitz constant.

According to the 👉Mean Value Theorem >>, for each fixed $t$, there is a $c$ between $y_1$ and $y_2$ such that
$$
\frac{f(t,y_1) - f(t,y_2)}{y_1 - y_2} = \frac{\partial f}{\partial y}(t,c)
$$
Therefore, $L$ can be taken to be the maximum of
$$
|\frac{\partial f}{\partial y}(t,c)|
$$
on the set.

The Lipschitz continuity hypothesis guarantees the existence and uniqueness of solutions of initial value problems.

THEOREM 6.2
Assume that $f(t,y)$ is Lipschitz continuous in the variable $y$ on the set $S = [a,b] \times [\alpha,\beta]$ and that $\alpha < y_a < \beta$. Then there exists $c$ between $a$ and $b$ such that the initial value problem
$$
\begin{cases}
y’ = f(t,y)\\
y(a) = y_a\\
t \in [a,c]
\end{cases}
\tag{6.11}
$$
has exactly one solution $y(t)$.
Moreover, if $f$ is Lipschitz on $[a,b] \times [-\infty,+\infty]$, then there exists exactly one solution on $[a,b]$.

THEOREM 6.3
Assume that $f(t,y)$ is Lipschitz in the variable $y$ on the set $S = [a,b] \times [\alpha,\beta]$. If $Y(t)$ and $Z(t)$ are solutions in $S$ of the differential equation
$$
y’ = f(t,y)
$$
with initial conditions $Y(a)$ and $Z(a)$ respectively, then
$$
|Y(t) - Z(t)| \leq e^{L(t-a)} |Y(a)-Z(a)|
\tag{6.13}
$$

==hard to understand…==

First-order linear equations

$$
\begin{cases}
y’ = g(t)y+h(t)\\
y(a) = y_a\\
t \in [a,b]
\end{cases}
$$

the explicit solution:

$$
y(t) = e^{\int g(t) dt} \int e^{-\int g(t) dt} h(t) dt
\tag{6.16}
$$

Analysis of IVP Solvers

A careful investigation of error in Euler’s Method will illustrate the issues for IVP solvers in general.

Local and global truncation error

The explicit Trapezoid Method

Taylor Methods

Systems of Ordinary Differential Equations

Higher order equations

Computer simulation: the pendulum

Computer simulation: orbital mechanics

Runge–Kutta Methods and Applications

The Runge–Kutta family

Computer simulation: the Hodgkin–Huxley neuron

Computer simulation: the Lorenz equations

Reality Check 6: The Tacoma Narrows Bridge

Variable Step-Size Methods

Embedded Runge–Kutta pairs

Order 4/5 methods

Implicit Methods and Stiff Equations

Multistep Methods

Generating multistep methods

Explicit multistep methods

Implicit multistep methods