Keywords: Metric Learning, deterministic forward kinematics (FK) layer, Procrustes alignment
Normalized Human Pose Features for Human Action Video Alignment_ICCV_2021
Jingyuan Liu 1 Mingyi Shi 2 Qifeng Chen 1 Hongbo Fu 3 Chiew-Lan Tai 1
1 The Hong Kong University of Science and Technology
2 The University of Hong Kong 3 The City University of Hong Kong

WorkFlow
Inspiration
A common approach to the problem of human action video alignment is to first estimate 2D or 3D human poses from two input videos, and then find the alignments by matching with features extracted from joint positions [48, 11], However, human poses still contain large variations in scale, bone length ratios, orientations, etc.
Global orientation normalization by Procrustes alignment(普氏对齐) is hard to be applied to in-the-wild videos when the ground-truth 3D poses are not available.
At first sight, a straightforward solution might be to compute joint angles from joint positions, and use raw joint angles [10] or their aggregations [35, 52] as features for matching.
However, the joint angle features suffer from information loss by dropping the skeleton’s relational context, which has a proven significance in capturing pose discrimination [8, 40].
To address the limitations in position-based and angular based pose representations, we propose to use a normalized human pose, an intermediate pose representation that reflects the pose information with respect to joint rotations, and is parameterized by joint positions to preserve the relational context of body configurations, as shown in Figure 1(c).
This normalized pose representation is enlightened by the recent works that use joint rotations as pose parameterizations for motion reconstruction [45] and pose sequence generation [53, 38].
They incorporate a deterministic forward kinematics (FK) layer in neural networks to convert the joint rotations into joint positions to avoid the joint rotation ambiguity problem in IK >>.
Methods
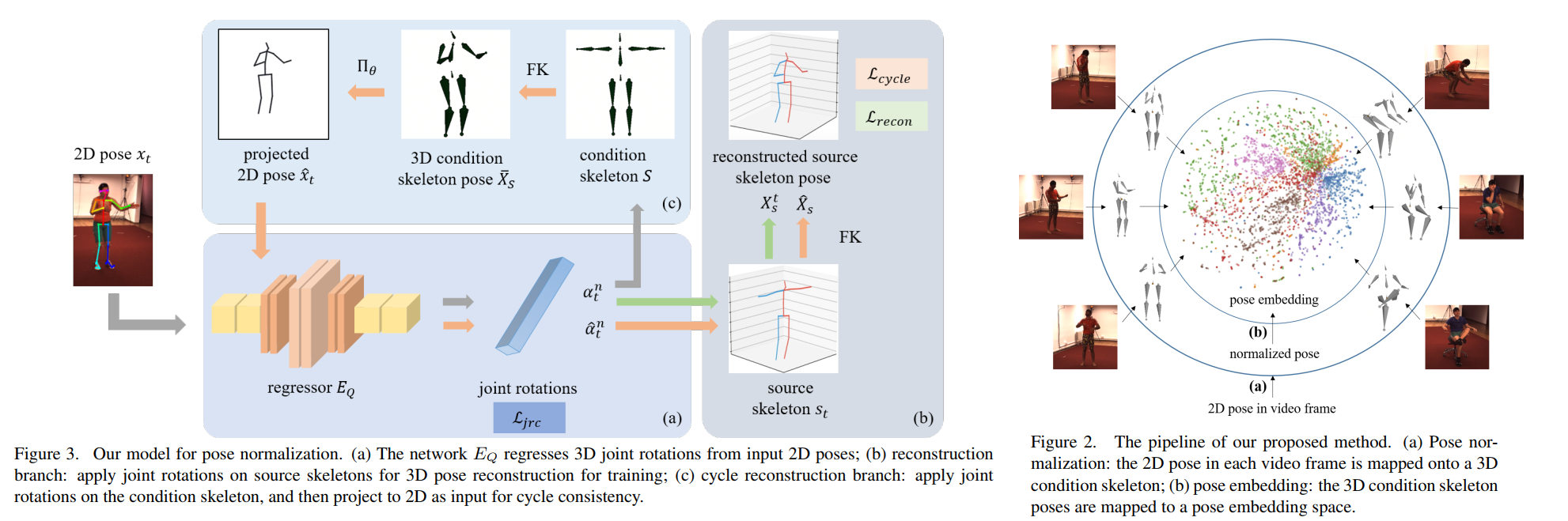
Pose Normalization
For a video containing $T$ frames, we denote the $2D$ position of joint $n$ at frame $t$ as $x^n_t
\in R^2, t = 1, 2, \cdots, T, n = 1, 2, \cdots, N$, where $N$ is the total number of joints.
The joint rotations, computed from the input $2D$ poses by $E_Q$, are represented as a unit quaternion >> for each joint $\alpha_t^n \in R^4$.
Denote the $FK$ process as
$$
X = FK(s, \alpha)
$$
where bones in a skeleton $s$ are rotated according to a set of joint rotations $\alpha$, resulting in the 3D joint positions $X$ of the skeleton.
In order to train $E_Q$, we apply the joint rotations $\alpha_t^n$ computed from 2D poses $x^n_t$ on two types of skeletons:
- the condition skeleton $S$, to facilitate the learning of pose normalization;
- the $3D$ source skeletons of the video subjects st computed from the ground-truth $3D$ poses, to assist the training of $E_Q$.
Reconstruction Branch
Applying $\alpha_t^n$ on the $3D$ source skeletons $s_t$ results in reconstructed $3D$ poses $X^t
_s$, which can be directly supervised by the groundtruth $3D$ poses $X_t^n$ using the reconstruction loss:
$$
\mathcal{L_{recon}} = \sum_{t_n} ||FK(s_t, \alpha_t^n) - X_t^n||^2
$$
Cycle Reconstruction Branch
The design of the cycle reconstruction branch is based on the observation that, since the condition skeleton has the same poses as the poses of the subject in the video frames, its projections should yield the same 3D joint rotations as the 3D joint rotations produced by the original input 2D poses.
However, applying rotations $\alpha_t^n$ on the condition skeleton results in new $3D$ poses $\bar{X_S}$ without paired groundtruth for supervised training. Thus, we adopt this cycle reconstruction that projects the $3D$ condition skeleton pose into $2D$ pose, and then compute $3D$ joint rotations from the projected $2D$ poses.
本质上来讲,就是经过这样一通操作,condition skeleton motion is the same with source skeleton motion though they may have different motion data, and the neural network $E_Q$ will become a model to infer correct condition skeleton rotation motion instead of source skeleton rotation motion.
The joint rotation consistency loss is computed as the differences between joint rotations from the input 2D poses and from the projected skeleton poses:
$$
\mathcal{L_{jrc}} = \sum_{t,n} ||\alpha_t^n - \hat{\alpha_t^n}||^2
$$
The cycle reconstruction loss is:
$$
\mathcal{L_{cycle}} = \sum_{t,n} ||FK(s_t, \hat{\alpha_t^n}) - X_t^n||^2
$$
Besides the above losses, we also adopted the foot contact loss $\mathcal{L_{fc}}$, which is commonly used in 3D pose estimations to reduce the skating effect [46].
The total loss function for training is:
$$
\mathcal{L} = \mathcal{L_{recon}} + \phi\mathcal{L_{cycle}} + \beta\mathcal{L_{jrc}} + \lambda\mathcal{L_{fc}}
$$
For inference, only the regressor $E_Q$ is used to compute the $3D$ joint rotations from $2D$ poses to be applied onto the condition skeleton.
Now we can understand the key idea of this paper:
- We design a neural network that learns to normalize human poses in videos. Specifically, the pose normalization network takes in $2D$ poses and estimate joint rotations, which are then applied by $FK$ on a pre-defined $3D$ skeleton with unified fixed bone lengths (called condition skeleton as in [53]).
- The joint rotations of the subjects’ poses in videos are thus converted into the joint positions of the condition skeleton to normalize the poses.
- In this way, the difference in joint positions of the condition skeleton is caused only by the difference in joint rotations.
- Since the normalized poses are not paired with ground-truth poses for training, our network adopted a cycle consistency training strategy (Section 3.2). With joint rotations, the poses can also be easily unified to the same global orientation by specifying the root joint rotation.
- Finally, the pose features are learned from the normalized $3D$ poses by metric learning. The resulting pose features are high-level human pose representations and can be directly compared by the Euclidean distance.
Pose Embedding
After the poses in the video frames are normalized into unified bone lengths and viewpoints, we use metric learning to map the poses to a pose embedding space to extract highlevel pose features.
深度学习的任务就是把高维原始数据(图像,句子)映射到低维流形,使得高维的原始数据被映射到低维流形之后变得可分,而这个映射就叫做Embedding, 或者这样理解, Embedding就是从原始数据提取出来的Feature,也就是那个通过神经网络映射之后的低维向量。
Ablation Study
Limitations
it extracts features from a complete normalized pose.(一个完整的归一化的姿态,也就是说不能有关节缺失) Future work includes modeling the normalized pose with partial observations. A potential solution that worth exploring is to adopt a probabilistic modeling with kinematics constraints [46, 23] as priors for the FK layer in the network, such that the missing joint positions would be filled by satisfying both kinematics
priors and non-missing joint positions.it requires ground-truth 3D joint positions in training.(需要在训练阶段有3d关节点的位置做ground-truth) Adopting weakly-supervised settings, such as using ordinal depths of joint pairs [36, 42] might enable training on in-the-wild datasets.
Classic Reference
[2]Andreas Aristidou, Daniel Cohen-Or, Jessica K Hodgins, Yiorgos Chrysanthou, and Ariel Shamir. Deep motifs and motion signatures. ACM Transactions on Graphics (TOG), 37(6):1–13, 2018. 3, 5
[10]Myung Geol Choi, Kyungyong Yang, Takeo Igarashi, Jun Mitani, and Jehee Lee. Retrieval and visualization of human motion data via stick figures. In Computer Graphics Forum, volume 31, pages 2057–2065. Wiley Online Library, 2012. 2, 3, 6, 8
[28]Julieta Martinez, Rayat Hossain, Javier Romero, and James J Little. A simple yet effective baseline for 3d human pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, pages 2640–2649, 2017. 1, 3, 5, 6, 7, 8
[56]Long Zhao, Xi Peng, Yu Tian, Mubbasir Kapadia, and Dimitris N. Metaxas. Semantic graph convolutional networks for 3d human pose regression. In IEEE Conference on Computer Vision and Pattern Recognition, pages 3425–3435, 2019. 5, 6, 7, 8
[48]Jennifer J Sun, Jiaping Zhao, Liang-Chieh Chen, Florian Schroff, Hartwig Adam, and Ting Liu. View-invariant probabilistic embedding for human pose. In European Conference on Computer Vision, pages 53–70. Springer, 2020. 1, 3, 6, 8
[24]Muhammed Kocabas, Nikos Athanasiou, and Michael J Black. Vibe: Video inference for human body pose and shape estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5253–5263, 2020. 3, 6, 8

