Keywords: Sketch Animation, ARAP, K-Shortest Path, Feature Tracking, ShapeContext
Live Sketch: Video-driven Dynamic Deformation of Static Drawings_CHI_2018
Qingkun Su 1, Xue Bai 3, Hongbo Fu 2, Chiew-Lan Tai 1, Jue Wang 3
1 Department of Computer Science and Engineering, HKUST
2 School of Creative Media, City University of Hong Kong
3 Megvii Inc. US
WorkFlow
Problem
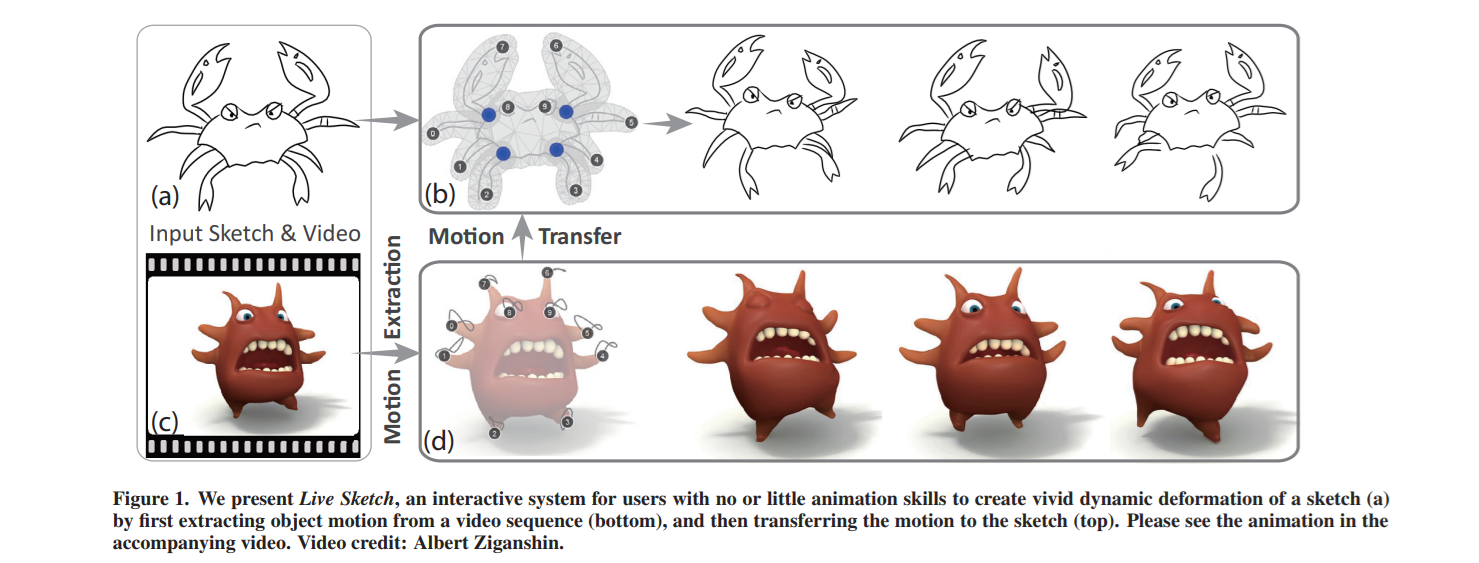
Creating sketch animations using traditional tools requires special artistic skills, and is tedious even for trained professionals.
To lower the barrier for creating sketch animations, we propose a new system, Live Sketch, which allows novice users to interactively bring static drawings to life by applying deformation-based animation effects that are extracted from video examples.
Innovation
motion extraction from video. We propose a new semiautomatic video tracking approach, which is able to track complex non-rigid object motion and is robust against occlusion遮挡 and ambiguity混淆.
video-to-sketch alignment.
and many-to-one motion driven sketch animation. A new stroke-preserving mesh deformation method for animating sketches, with constraints for better preserving the shape of user-specified strokes.
Methods
Control Point Extraction
We have tried to use image features such as SIFT or SURF to find good points to track, and also explored determining the points based on the initial object shape. In the end we conclude that although these automatic approaches do work well in some cases, they cannot handle a wide variety of
examples well.
The control points are mainly rely on user specification
Motion Extraction
We first adopt a dynamic-programming-based trajectory optimization framework [2, 11] to track individual points.
![]()
KLT point tracker [53]. these methods may fail for some points that are hard to track, e.g., points specified in textureless regions, resulting in drifting.
When tracking drifting occurs for one point, the user only needs to modify the tracking position of the failed point in a particular frame, which is incorporated as a hard constraint to globally refine the whole trajectory of the failed point.
Therefore, the user can quickly refine the tracking results by only editing a few frames. This interactive tracking method is quite efficient and is able to address drifting due to occlusion.
Specifically, the tracking algorithm optimizes the following energy for each control point trajectory:
$$
E_{tr}(x) = \sum_t (\lambda_d d(x_t, x_{t+1}) + \lambda_u u(p_t, p_{t+1}) + \underset{k}{min}(a(p_t,c_k)))
\tag{1}
$$
where $x_t$ represents the position of a control point $x$ in frame $t$, and $p_t$ denotes the feature descriptor (SIFT in our implementation) of the image patch (we use $9 \times 9$ patches) centered at $x_t$.
The velocity term:
$$
d(\cdot) = ||x_t, x_{t+1}||_2^2
$$
update penalty term:
$$
u(\cdot) = ||p_t, p_{t+1}||_2^2
$$
these two terms measure the respective motion intensity and appearance variation between two consecutive frames, to achieve a smooth motion and appearance transition.
the third term:
$$
a(\cdot) = ||p_t,q_k||_2^2
$$
is a measure of the appearance deviation from the user specified control point locations ${c_k}$, where $q_k$ is the patch feature descriptor of $c_k$.
The user may manually specify two or more control point positions at different frames. We measure the appearance energy of points at other frames $\underset{k}{min}(a(p_t,c_k))$, so that they should match at least one of these user-specified control points.
We minimize the energy function in Eq. 1, by finding the shortest path of a graph (Fig. 4).
The weight of each edge is computed by
$$
w_e(p_t, p_{t+1}) = \lambda_d d(x_t, x_{t+1}) + \lambda_u u(p_t, p_{t+1})
$$
To handle the occlusion problem, we also fully connect the points of each frame with those of its next m frames (dot lines in Fig. 4, we set m = 10).
The weight of the extra edge between two respective nodes $p_t$ and $p_t’$ of frame $t$ and $
t’, (t + 1 < t’ \leq t + m)$ is
$$
w_e(p_t, p_{t’}) = \lambda_o + \lambda_d d(x_t, x_{t’}) + (t’ - t)\lambda_u u(p_t, p_{t’})
$$
本质上就是给出edge weight,图论中的起点到终点的最短路径, Dijkstra似乎就可以呀
Another problem is drifting by ambiguity.
![]()
To solve this problem, we propose a new energy minimization method to jointly optimize the tracking trajectories of multiple points (Fig 5). The main idea is to first generate a set of
trajectories for each control point as candidate trajectories (Fig. 5(top)) and then employ a global optimization approach to select the best one for each point by jointly considering multiple points together.
we apply the method proposed in [16] to compute a set of candidate tracking trajectories.(k-shortest path)
We jointly optimize over multiple tracking points to find the best trajectory for each point. This can be formulated as the following energy minimization problem:
$$
arg min \sum_i E_{tr}(x^i) + \beta \sum_{i \neq j} E_o(x^i, x^j)
\tag{2}
$$
$E_o(x^i, x^j)$ is defined as the normalized duration of the overlapping portion of the two trajectories. Intuitively, this term prevents two similar control points to collapse into a single one, in which case the overlapping portion of the two trajectories will be large.
We use a greedy algorithm to minimize this energy. We first initialize the solution by choosing the trajectory that has the minimal tracking energy for each point (according to Eq. 1).
Starting from the point that has the largest total energy according to Eq. 2, we assign to it another candidate trajectory that best minimizes this energy. We repeat this process until the total energy cannot be further reduced.
Control Point Transfer
The contour of the sketch can be extracted using the Active Contour models [26].
The contour of the video object can be extracted by automatic GrabCut segmentation [37] with the bounding box enclosing all the tracking points as input.Otherwise, the user can quickly draw the correct outline using a pen tool (e.g., the example in Fig. 6(bottom)).
Then we apply the Shape Context method [7] to build correspondence between the two contours.
Next, for a control point inside the video object, we represent its location using the barycentric coordinate of a set of evenly sampled contour points, and compute its location using the same barycentric coordinate on the sketch image.
Motion Transfer
Traditional controlled mesh deformation methods, such as the as-rigid-as-possible (ARAP) mesh deformation [24, 25], are designed to keep only the rigidity of the mesh triangles (see
Fig.8)
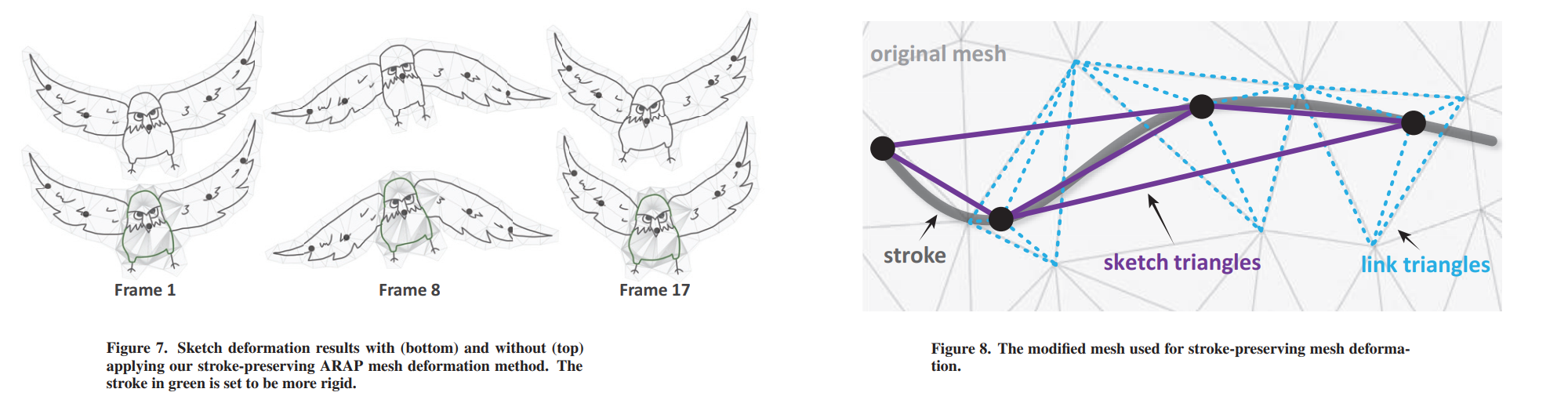
Our method adds new mesh triangles derived from the input strokes to the original mesh.
Original mesh, shown in gray in Figure8.
$$
\mathcal{M_0} = (\mathcal{V_0, J_0})
$$
uniformly sample points from each user-specified input stroke, and construct a sketch triangle set, purple in Figure8.
$$
\mathcal{M_s} = (\mathcal{V_s, J_s})
$$
construct a link triangle set $\mathcal{J_l}$ by connecting each vertex in $\mathcal{V_s}$ with the three vertices of the triangle in $\mathcal{V_0}$ on which it falls.
Give the augumented mesh structure,
$$
\mathcal{M} = (\mathcal{V_0 \cup V_s, J_0 \cup J_s \cup J_l})
$$
we formulate the stroke-preserving ARAP deformation as the following energy minimization problem:
$$
\underset{\mathcal{M}}{min} E_0 + \gamma_l E_{link} + \gamma_s E_{sketch}
\tag{3}
$$
where $E_0$, $E_{link}$ and $E_{sketch}$ are the deformation energy terms of the three mesh triangles set $\mathcal{J_0}$, $\mathcal{J_l}$ and $\mathcal{J_s}$, respectively. Each energy term is defined as:
$$
E(\mathcal{J}) = \sum_{t \in \mathcal{J}} \sum_{v_i,v_j \in t} || \overrightarrow{v_i’v_j’} - H \overrightarrow{v_iv_j}||^2
\tag{4}
$$
which is based on [24]. It can also be formulated by other ARAP optimization methods, like [25].
H is a rigid and scale irrelevant ARAP transformation matrix, which is achieved by a two-step optimization algorithm.
Minimizing $E_{sketch}$ keeps the shape of the strokes while minimizing $E_{link}$ transfers the deformation of the original mesh to the strokes.
Multiple-Layer Animation
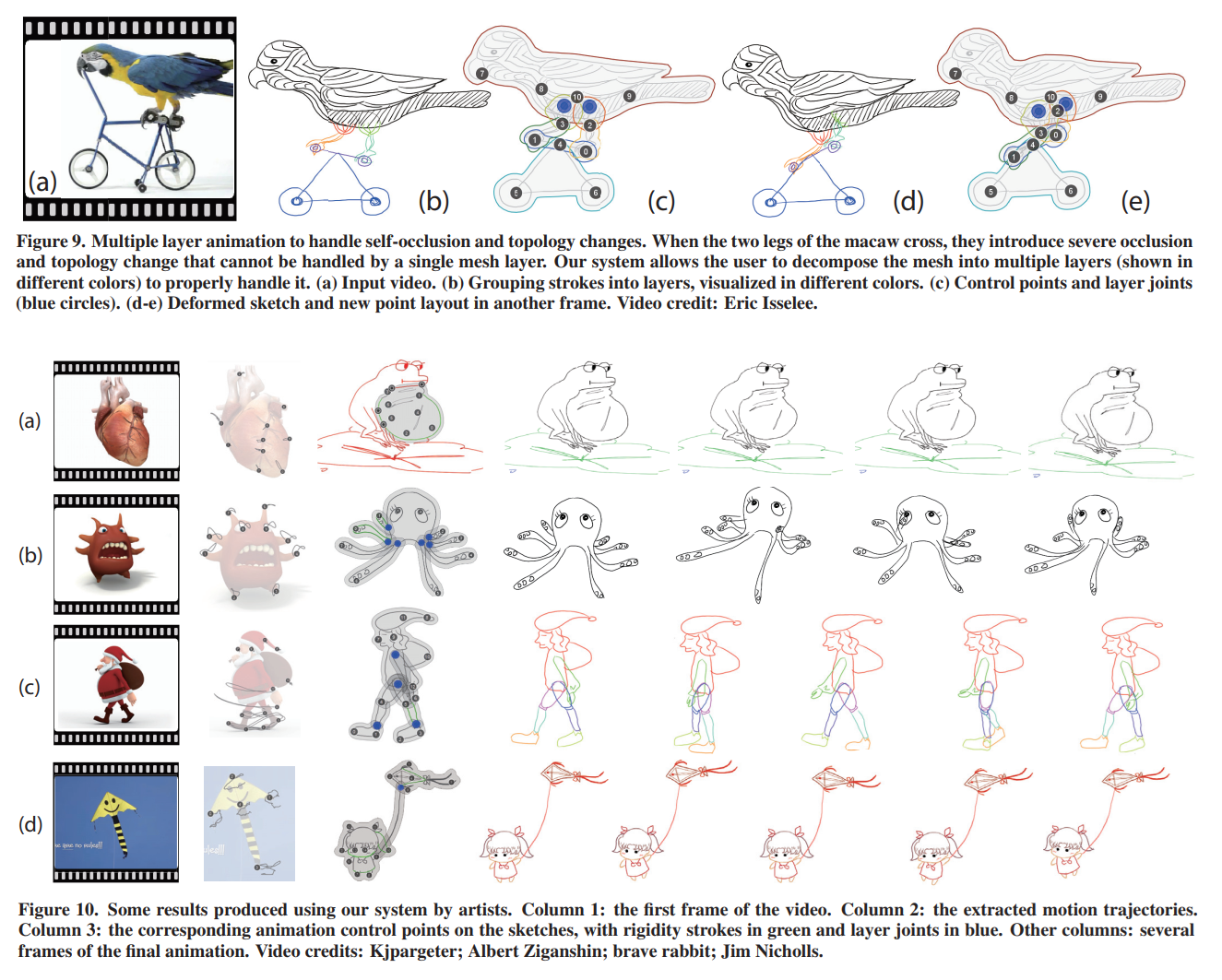
As discussed earlier, single layer, mesh-deformation-based animation cannot handle topology change, which is common for dynamic objects (see Fig. 9a). To handle such cases, our system allows the user to create animations with multiple layers.
To avoid detaching different layers from each other during animation, our system then automatically detects the intersections of these layers, and adds one joint point at the center of each intersection region (Fig. 9c, blue circles) so that these layers are connected.
Classic Reference
[53]. Alper Yilmaz, Omar Javed, and Mubarak Shah. 2006. Object tracking: A survey. Acm computing surveys (CSUR) 38, 4 (2006), 13.
[2]. B. Amberg and T. Vetter. 2011. GraphTrack: Fast and globally optimal tracking in videos. In CVPR 2011. 1209–1216.
[11]. A. Buchanan and A. Fitzgibbon. 2006. Interactive Feature Tracking using K-D Trees and Dynamic Programming. In CVPR’06, Vol. 1. 626–633.
[16]. Theodoros Chondrogiannis, Panagiotis Bouros, Johann Gamper, and Ulf Leser. 2015. Alternative routing: k-shortest paths with limited overlap. In SIGSPATIAL GIS ’15. ACM, 68.
[26]. Michael Kass, Andrew Witkin, and Demetri Terzopoulos. 1988. Snakes: Active contour models. IJCV 1, 4 (1988), 321–331.
[37]. Carsten Rother, Vladimir Kolmogorov, and Andrew Blake. 2004. “GrabCut”: Interactive Foreground Extraction Using Iterated Graph Cuts. ACM Trans. Graph. 23, 3 (Aug. 2004), 309–314
[7]. Serge Belongie, Jitendra Malik, and Jan Puzicha. 2000. Shape context: A new descriptor for shape matching and object recognition. In Nips, Vol. 2.
[24]. Takeo Igarashi, Tomer Moscovich, and John F. Hughes. 2005. As-rigid-as-possible Shape Manipulation. In ACM Trans. Graph., Vol. 24. 1134–1141.
[25]. Alec Jacobson, Ilya Baran, Jovan Popovic, and Olga Sorkine. 2011. Bounded Biharmonic Weights for Real-time Deformation. In SIGGRAPH ’11. ACM, Article 78, 8 pages.

