Keywords: Curve Fitting to Strokes, Variational Optimization, Cluster Strokes, C++
https://www.cs.ubc.ca/labs/imager/tr/2021/StrokeStrip/

WorkFlow
Inspiration
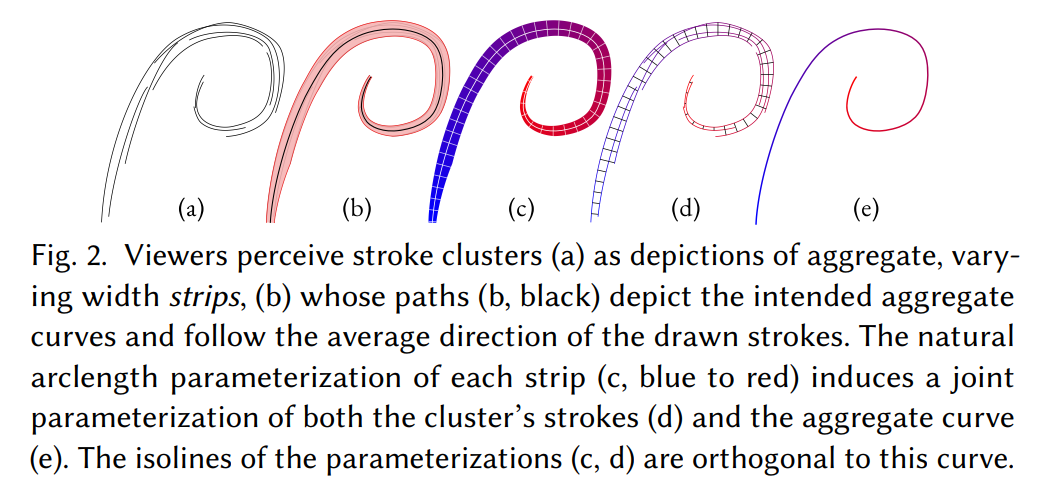
We achieve this goal by leveraging insights about human perception of stroke clusters.
Challenges
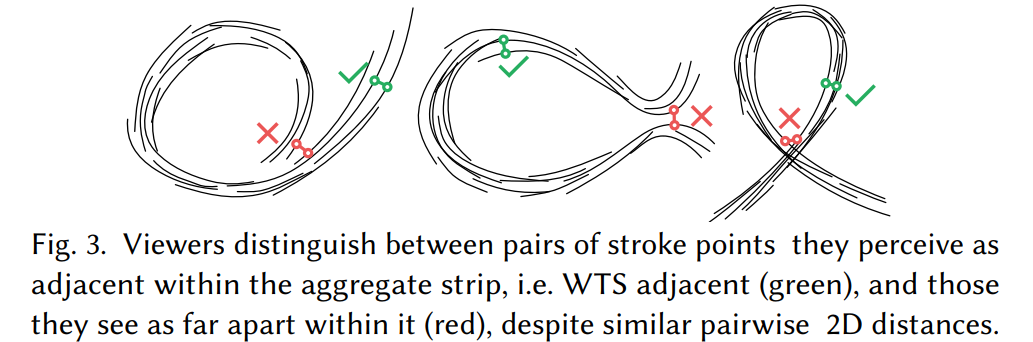
we do not know which points on different strokes that are adjacent in Euclidean space are perceived as WTS adjacent. our algorithm needs to compute these crosssections given only the raw strokes as input.
We consequently face two interconnected challenges:
we must compute optimal isovalues along each cluster cross-section while simultaneously computing the cross-sections themselves.
Address the Challenges
We robustly address both challenges at once by casting the computation of the parameterization and the underlying isoline crosssections as a constrained variational problem. We then solve it using a combined discrete-continuous optimization framework.
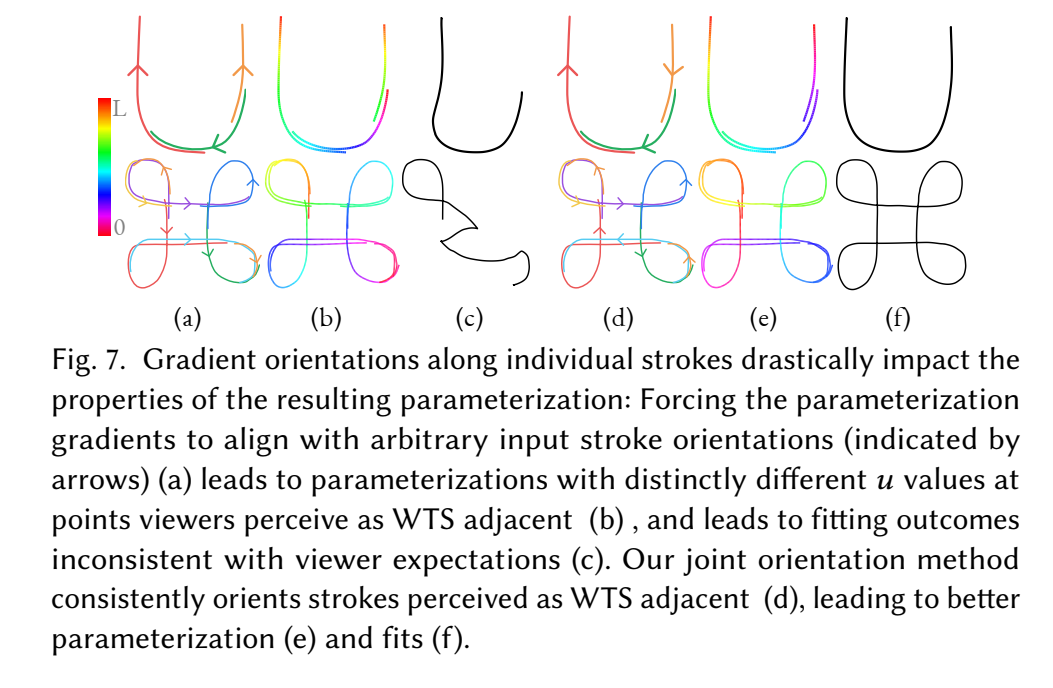
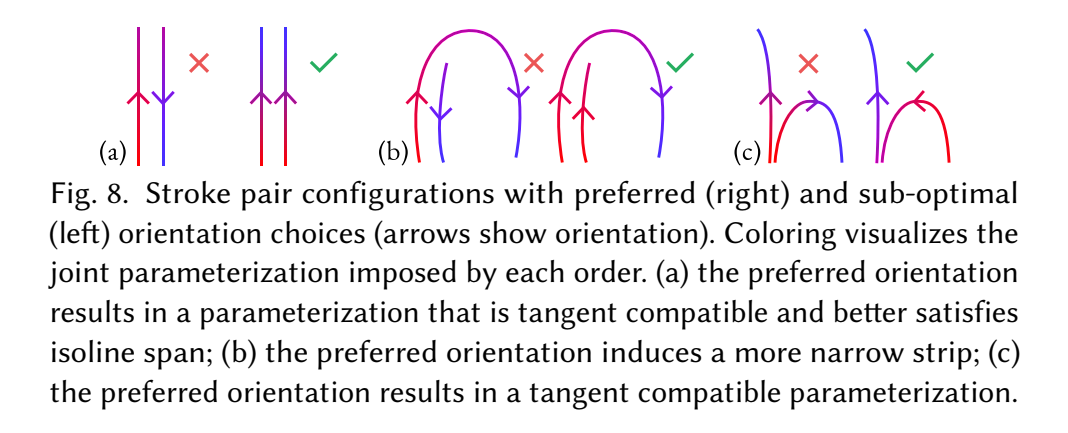
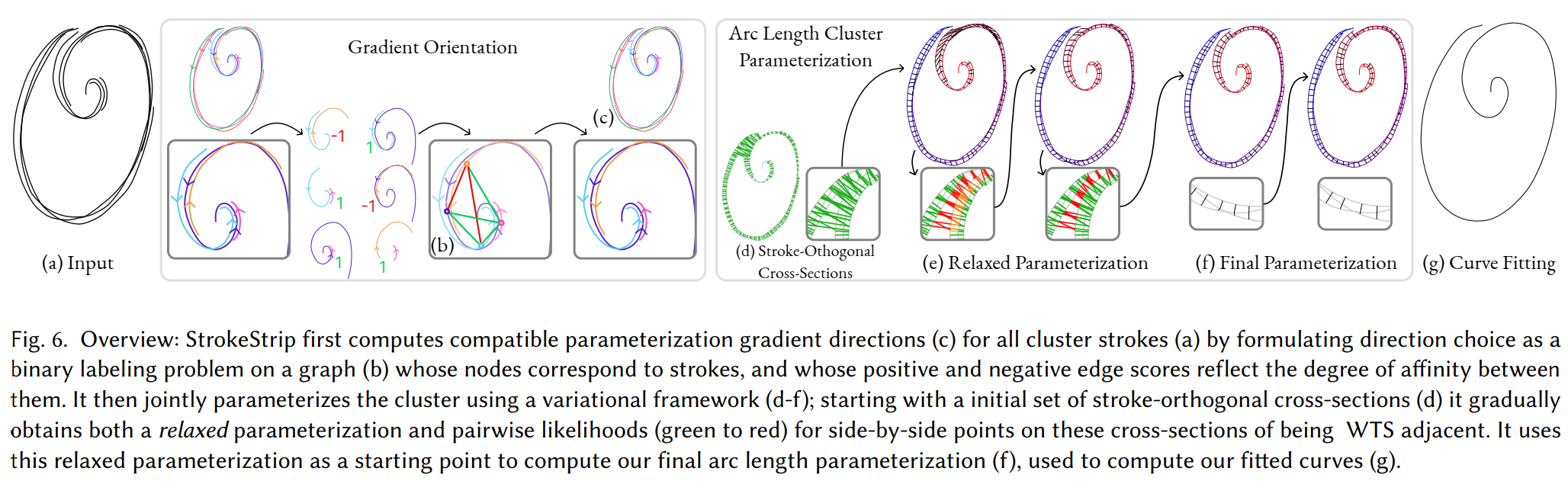
- Step1. determine the optimal orientations of parameterization gradients along each stroke(决定沿着每个笔画的最优梯度(参数化)朝向), converting monotonicity constraints into more tractable inequality ones(把单调约束转化为更容易解决的不等式问题)
- Step2. jointly solve for cluster cross-sections and parameter values along them using a variational optimization framework(使用变分优化框架联合解决等值线和沿着等值线的参数值)
The Main Process
Some Definitions
A strip is well described by its centerline $\gamma(t) \in R^2$, parameterized by its arclength $t \in [0, L]$, and width $W(t)$
The two sides of a strip are then the two curves at the distance of $W(t)/2$ from the centerline in the normal direction, or more formally $\gamma(t) \pm \frac{W(t)}{2}n(t)$.
Simply put, it is a function $u(x)$ defined for all points in the strip, such that straight line segments $C(t) = \lbrace \gamma(t) + an(t)| a \in [-\frac{W(t)}{2}, \frac{W(t)}{2}]\rbrace$ are the parameterization’s isolines(等值线,和中心线正交的线).
$t = u(x), x ∈ C(t)$.
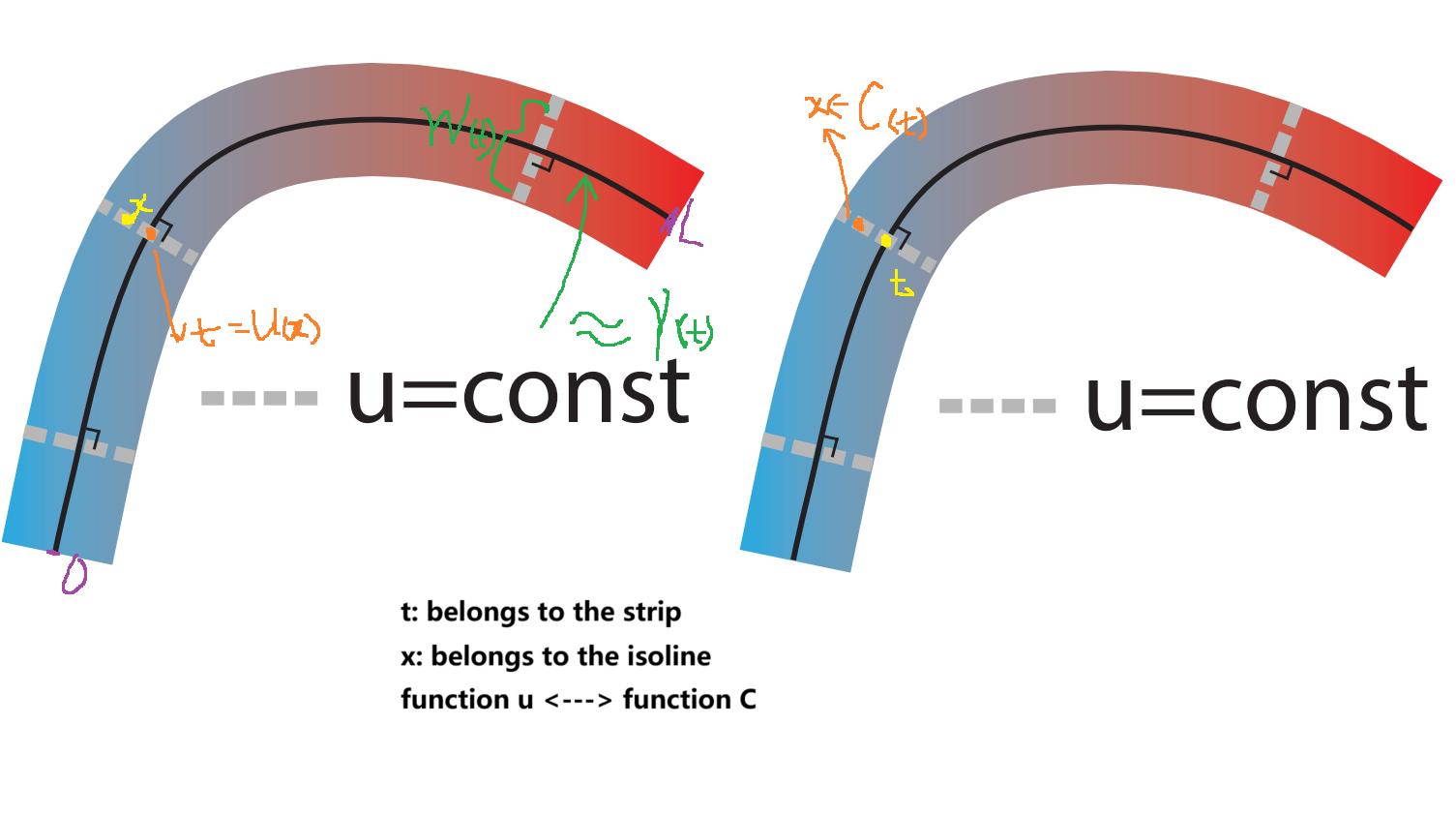
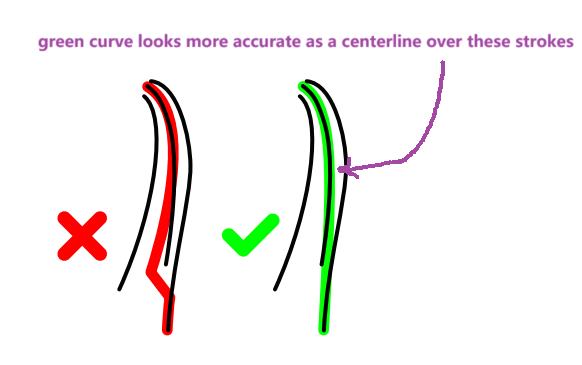
centerline tangent $\tau(t)$, about the centerline, we prioritize tangent alignment over centrality when computing the strip parameterizations and paths.
thus, given the oriendted strokes $S = \lbrace s_i, i = 1, \cdots, N\rbrace$, we are looking for a map(映射)
$$
u(x): U_iS_i \mapsto [0;L]
$$
For a non self-intersecting strip $S \subset R^2$, its arc length parameterization $u: S \rightarrow R$ is the minimizer of the following variational problem:
$$
\underset{u}{min} \int_0^L ||\frac{1}{W(t)} \int_{C(t)} \nabla u(x)dx - \tau(t)||^2dt
$$
GRADIENT ORIENTATION