Keywords: Coordinate Space, Transformation, Matrix, Quaternions, Polar Coordinate System
This is the partly ReadingNotes from book 3D Math Primer for Graphics and Game Development 2nd Edition.
Attetion: left-hand rule, row vectors, right multiply.
🌟Deduce the Projection and Rotation Matrix
Perspective Projection Matrix
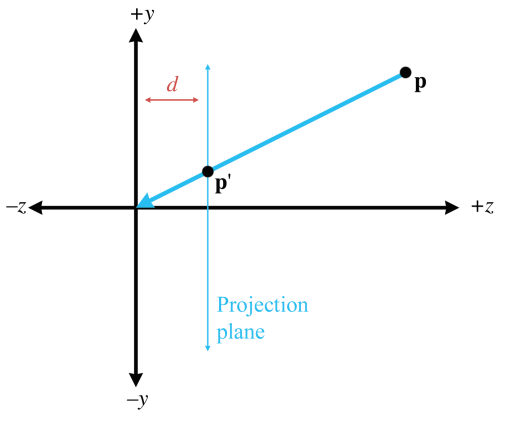
from the picture above, the camera is at origin $(0,0,0)$, the projection plane is $z = d$ (also, the Focus distance is $d$), by similar triangles, we can see that
$$
\frac{p_y’}{d} = \frac{p_y}{z}
\Rightarrow p_y’ = \frac{dp_y}{z}, also \space p_x’ = \frac{dp_x}{z}
$$
so
$$
p = \begin{bmatrix} x & y & z \end{bmatrix}
\longmapsto
\begin{aligned}
p’ &= \begin{bmatrix} \frac{dx}{z} & \frac{dy}{z} & \frac{dz}{z} \end{bmatrix}\\
&= \frac{\begin{bmatrix} x & y & z \end{bmatrix}}{z/d}
\end{aligned}
$$
So we need a $4 \times 4$ matrix that multiplies a homogeneous vector $[x, y, z, 1]$ to produce $[x, y, z, z/d]$. The matrix that does this is
$$
\begin{bmatrix}
x & y & z & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1/d\\
0 & 0 & 0 & 0
\end{bmatrix}
=
\begin{bmatrix}
x & y & z & z/d
\end{bmatrix}
$$
Multiplication by this matrix doesn’t actually perform the perspective transform, it just computes the proper denominator into $w(w = z/d)$. Remember that the perspective division actually occurs when we convert from $4D$ to $3D$ by dividing by $w$.
Orthogonal Projection Matrix
Rotation Matrix
3D Rotation about Cardinal Axes
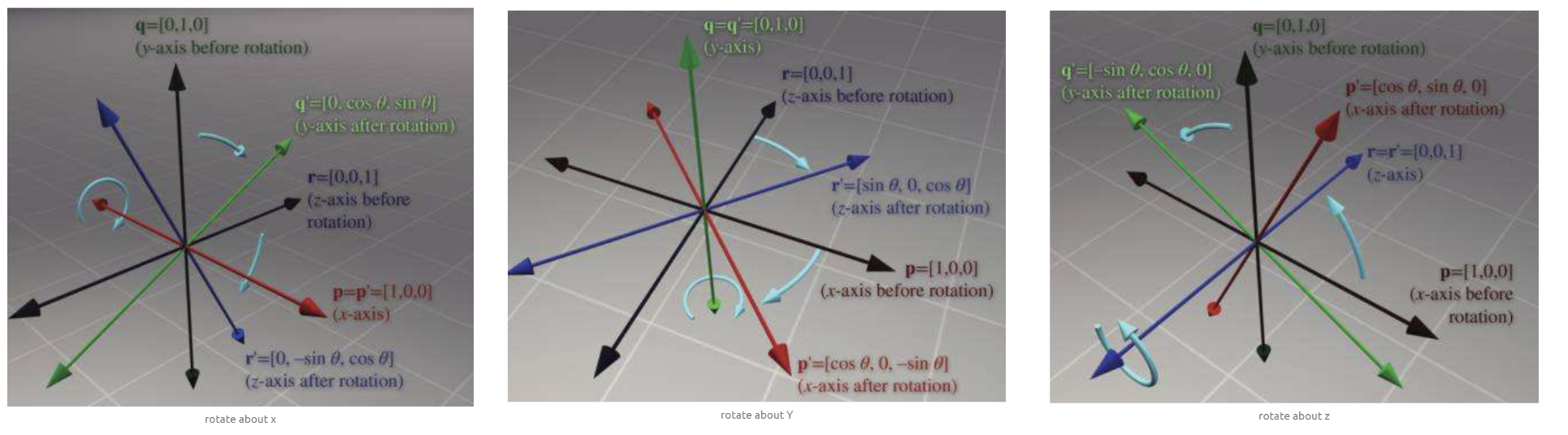
matrix to rotate about the $x-axis$:
$$
R_x(\theta) =
\begin{bmatrix}
1 & 0 & 0\\
0 & \cos\theta & \sin \theta\\
0 & -\sin \theta & \cos \theta
\end{bmatrix}
$$
matrix to rotate about the $y-axis$:
$$
R_y(\theta) =
\begin{bmatrix}
\cos\theta & 0 & -\sin\theta \\
0 & 1 & 0\\
\sin\theta & 0 & \cos\theta
\end{bmatrix}
$$
matrix to rotate about the $z-axis$:
$$
R_z(\theta) =
\begin{bmatrix}
\cos\theta & \sin\theta & 0\\
-\sin\theta & \cos\theta & 0\\
0 & 1 & 0
\end{bmatrix}
$$
3D Rotation about Arbitrary Axis
Let’s derive a matrix to rotate about $\widehat{\vec{n}}$ by the angle $\theta$. that means:
$$
\vec{v}’ = \vec{v}R(\widehat{\vec{n}},\theta)
$$
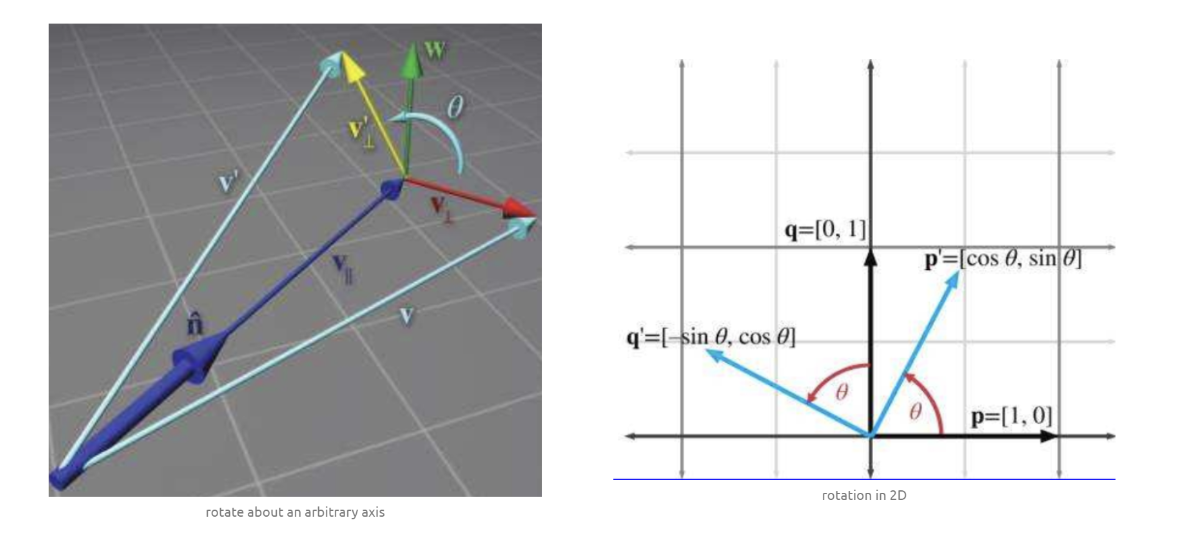
The basic idea is to solve the problem in the plane perpendicular to $\widehat{\vec{n}}$.
we separate $\vec{v}$ into two vectors, $\vec{v_{\parallel}}$ and $\vec{v_{\perp}}$, which are parallel and perpendicular to $\vec{v}$, respectively, such that $\vec{v} = \vec{v_{\parallel}} + \vec{v_{\perp}}$.
By rotating each of these components individually, we can rotate the vector as a whole. In other words, $\vec{v’} = \vec{v_{\parallel}’} + \vec{v_{\perp}’}$.
Since $\vec{v_{\parallel}}$ is parallel to $\widehat{\vec{n}}$, it will not be affected by the rotation about $\widehat{\vec{n}}$. In other words, $\vec{v_{\parallel}’} = \vec{v_{\parallel}}$. So all we need to do is compute $\vec{v_{\perp}’}$, and then we have $\vec{v’} = \vec{v_{\parallel}’} + \vec{v_{\perp}’}$.
To compute $\vec{v_{\perp}’}$ , we construct the vectors $\vec{v_{\parallel}}$ and $\vec{v_{\perp}}$ and an intermediate vector $\vec{w}$, The vector $\vec{w}$ is mutually perpendicular to $\vec{v_{\parallel}}$ and $\vec{v_{\perp}}$ and has the same length as $\vec{v_{\perp}}$:
$$
\begin{aligned}
\vec{v_{\parallel}} &= (\vec{v} \cdot \widehat{\vec{n}})\widehat{\vec{n}}\\
\vec{v_{\perp}} &= \vec{v} - \vec{v_{\parallel}} \\
&= \vec{v} - (\vec{v} \cdot \widehat{\vec{n}})\widehat{\vec{n}} \\
\vec{w} &= \widehat{\vec{n}} \times \vec{v_{\perp}} \\
&= \widehat{\vec{n}} \times (\vec{v} - \vec{v_{\parallel}})\\
&= \widehat{\vec{n}} \times \vec{v} - \widehat{\vec{n}} \times \vec{v_{\parallel}}\\
&= \widehat{\vec{n}} \times \vec{v}
\end{aligned}
$$
How do these vectors help us compute $\vec{v_{\perp}’}$?
Notice that $\vec{w}$ and $\vec{v_{\perp}}$ form a 2D coordinate space, with $\vec{v_{\perp}}$ as the $“x-axis”$ and $\vec{w}$ as the $“y-axis”$. (Note that the two vectors don’t necessarily have unit length.)
$\vec{v_{\perp}’}$ is the result of rotating $\vec{v’}$ in this plane by the angle $θ$. Remember the endpoints of a unit ray rotated by an angle $\theta$ are $\cos\theta$ and $\sin\theta$?
$$
\begin{aligned}
\vec{p’} &= \cos \theta \vec{e_1} + \sin \theta \vec{e_2} \\
&= \cos\theta \begin{bmatrix} 1 & 0\end{bmatrix} + \sin\theta \begin{bmatrix} 0 & 1\end{bmatrix}\\
&= \begin{bmatrix} \cos\theta & 0\end{bmatrix} + \begin{bmatrix} 0 & \sin\theta\end{bmatrix} \\
&= \begin{bmatrix} \cos\theta & \sin\theta \end{bmatrix}
\end{aligned}
$$
The only difference here is that our ray is not a unit ray, and we are using $\vec{v_{\perp}}$ and $\vec{w}$ as our basis vectors. Thus, $\vec{v_{\perp}’}$ can be computed as
$$
\begin{aligned}
\vec{v_{\perp}’} &= \cos\theta \vec{v_{\perp}} + \sin\theta \vec{w}\\
&= \cos\theta (\vec{v} - (\vec{v} \cdot \widehat{\vec{n}})\widehat{\vec{n}}) + \sin\theta (\widehat{\vec{n}} \times \vec{v})
\end{aligned}
$$
Thus,
$$
\begin{aligned}
\vec{v’} &= \vec{v_{\parallel}’} + \vec{v_{\perp}’} \\
&= \cos\theta (\vec{v} - (\vec{v} \cdot \widehat{\vec{n}})\widehat{\vec{n}}) + \sin\theta (\widehat{\vec{n}} \times \vec{v}) + (\vec{v} \cdot \widehat{\vec{n}})\widehat{\vec{n}}
\end{aligned}
\tag{5.1}
$$
the remaining arithmetic is essentially a notational change that expresses Equation (5.1) as a matrix multiplication.
Now that we have expressed $\vec{v’}$ in terms of $\vec{v}, \widehat{\vec{n}}$ and $θ$. we can compute what the basis vectors are after transformation and construct our matrix.
$$
\vec{e_1} = \begin{bmatrix} 1 & 0 & 0\end{bmatrix}
\longmapsto
\vec{e_1’} =
\begin{bmatrix}
n_x^2(1-\cos\theta) + \cos\theta\\
n_x n_y(1-\cos\theta) + n_z \sin\theta\\
n_x n_z(1-\cos\theta) - n_y\sin\theta
\end{bmatrix}^T
$$
$$
\vec{e_2} = \begin{bmatrix} 0 & 1 & 0\end{bmatrix}
\longmapsto
\vec{e_2’} =
\begin{bmatrix}
n_x n_y(1-\cos\theta) - n_z \sin\theta\\
n_y^2(1-\cos\theta) + \cos\theta\\
n_y n_z(1-\cos\theta) + n_x\sin\theta
\end{bmatrix}^T
$$
$$
\vec{e_3} = \begin{bmatrix} 0 & 0 & 1\end{bmatrix}
\longmapsto
\vec{e_3’} =
\begin{bmatrix}
n_x n_z(1-\cos\theta) + n_y\sin\theta\\
n_y n_z(1-\cos\theta) - n_x \sin\theta\\
n_z^2(1-\cos\theta) +\cos\theta
\end{bmatrix}^T
$$
Thus
$$
\begin{aligned}
R(\widehat{\vec{n}},\theta) &=
\begin{bmatrix}
R(\vec{e_1}) & R(\vec{e_2}) & R(\vec{e_3’})
\end{bmatrix}^T\\
&=
\begin{bmatrix}
\vec{e_1’} & \vec{e_2’} & \vec{e_3’}
\end{bmatrix}^T\\
&=
\begin{bmatrix}
n_x^2(1-\cos\theta) + \cos\theta & n_x n_y(1-\cos\theta) + n_z \sin\theta & n_x n_z(1-\cos\theta) - n_y\sin\theta\\
n_x n_y(1-\cos\theta) - n_z \sin\theta & n_y^2(1-\cos\theta) + \cos\theta & n_y n_z(1-\cos\theta) + n_x\sin\theta\\
n_x n_z(1-\cos\theta) + n_y\sin\theta & n_y n_z(1-\cos\theta) - n_x \sin\theta & n_z^2(1-\cos\theta) +\cos\theta
\end{bmatrix}
\end{aligned}
$$
👉How to understand Basis in Linear Algebra >>
👉How to understand Basis and Coordinate Systems in Linear Algebra >>
👉How to understand Basis and Coordinate Systems and Coordinate Mapping in Linear Algebra >>
Quaternion
🌟Deduce Quaternion
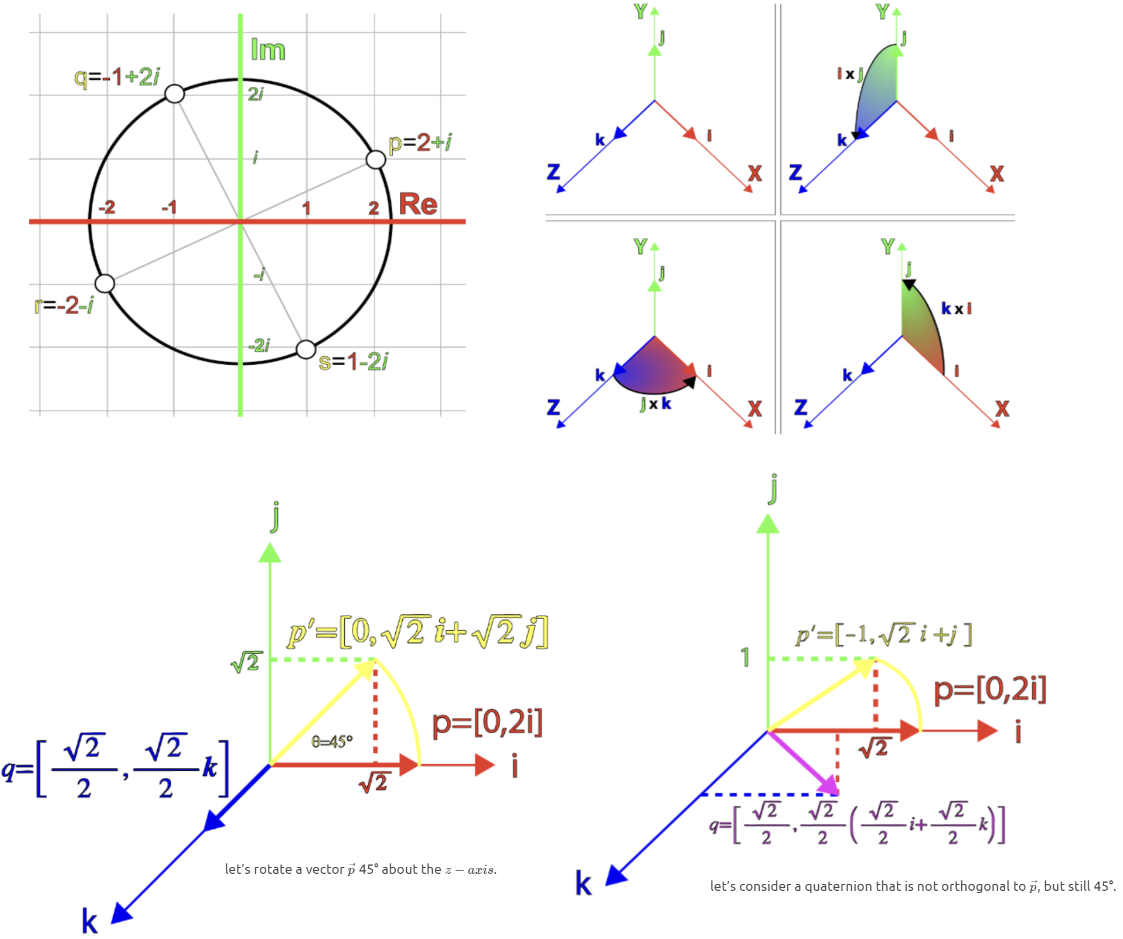
we can say that if we multiply a complex number by $i$, we can rotate the complex number through the complex plane at 90° increments.
$$
\begin{aligned}
p &= 2 + i\\
q &= pi\\
&= -1+2i\\
r &= qi\\
&= -2-i\\
s &= ri\\
&= 1-2i\\
t &= si\\
&= 2 + i
\end{aligned}
$$
Rotate a point through the 2D complex plane as
$$
q = \cos\theta + i \sin\theta
$$
Then,
$$
\begin{aligned}
p &= a + bi\\
pq &= (a+bi)(\cos\theta + i \sin\theta)\\
&= a\cos\theta - b\sin\theta + (a\sin\theta + b\cos\theta)i
\end{aligned}
$$
Written in matrix form:
$$
\begin{bmatrix}
a’ & -b’\\
b’ & a’
\end{bmatrix}
=
\begin{bmatrix}
\cos\theta & -\sin\theta\\
\sin\theta & \cos\theta
\end{bmatrix}
\begin{bmatrix}
a & -b\\
b & a
\end{bmatrix}
$$
Which is the method to rotate an arbitrary point in the complex plane counter-clockwise about the origin.
The general form to express quaternions is
$$
\begin{aligned}
\pmb{q} &= s + xi + yj + zk, s,x,y,z\in R\\
&= [s,\vec{v}]
\end{aligned}
$$
Let express a quaternion that can be used to rotate a point in 3D-space as such:
$$
\pmb{q} = [\cos\theta, \sin\theta\vec{v}]
$$
let $\pmb{p}$ as a Pure quaternion in the form, $\pmb{q}$ is a unit-norm quaternion:
$$
\pmb{p} = [0,\vec{p}], \pmb{q} = [s, \lambda \hat{\vec{v}}]
$$
Then,
$$
\begin{aligned}
\pmb{p’} &= \pmb{qp}\\
&= [s, \lambda \hat{\vec{v}}][0,\vec{p}]\\
&= [-\lambda \hat{\vec{v}} \cdot \vec{p}, s\vec{p}+ \lambda \hat{\vec{v}} \times \vec{p}]
\end{aligned}
$$
First, think special case $\vec{p} \perp \hat{\vec{v}}$, so the result becomes Pure quaternion:
$$
\pmb{p’} = [0, s\vec{p}+ \lambda \hat{\vec{v}} \times \vec{p}]
$$
In this case, to rotate $\vec{p}$ about $\hat{\vec{v}}$ we just substitute $s = \cos\theta$ and $\lambda = \sin\theta$.
$$
\pmb{p’} = [0, \cos\theta \vec{p}+ \sin \theta \hat{\vec{v}} \times \vec{p}]
$$
💡For example💡: let’s rotate a vector $\vec{p}$ 45° about the $z-axis$.
our quaternion $\pmb{q}$ is:
$$
\begin{aligned}
\pmb{q} &= [\cos\theta, \sin\theta \vec{k}]\\
&= [\frac{\sqrt 2}{2}, \frac{\sqrt 2}{2} \vec{k}]
\end{aligned}
$$
let $\vec{p} \perp \vec{k}$, so
$$
\pmb{p} = [0, 2\vec{i}]
$$
Thus,
$$
\begin{aligned}
\pmb{p’} &= \pmb{qp}\\
&= [\frac{\sqrt 2}{2}, \frac{\sqrt 2}{2} \vec{k}][0, 2\vec{i}]\\
&= [0, \frac{\sqrt 2}{2} \vec{i} + \frac{\sqrt 2}{2} \vec{j}]
\end{aligned}
$$
$$
|\pmb{p’}| = 2
$$
💡For example💡 let’s consider a quaternion that is not orthogonal to $\vec{p}$, but still 45°.
$$
\begin{aligned}
&\hat{\vec{v}} = \frac{\sqrt 2}{2}\vec{i} + \frac{\sqrt 2}{2}\vec{k}\\
&\vec{p} = 2\vec{i}\\
&\pmb{q} = [\cos\theta, \sin\theta \hat{\vec{v}}]\\
&\pmb{p} = [0,\vec{p}]
\end{aligned}
$$
Thus,
$$
\begin{aligned}
\pmb{p’} &= \pmb{qp}\\
&= [\cos\theta, \sin\theta \hat{\vec{v}}][0,\vec{p}]\\
&= [-1, \sqrt 2 \vec{i} + \vec{j}]
\end{aligned}
$$
But, the norm has changed, that’s not we want.
$$
|\pmb{p’}| = \sqrt 3
$$
Hamilton recognized (but didn’t publish) that if we post-multiply the result of $\pmb{qp}$ by the inverse of $\pmb{q}$ then the result is a pure quaternion and the norm of the vector component is maintained.
so,
$$
\begin{aligned}
\pmb{q} &= [\cos\theta, \sin\theta \hat{\vec{v}}]\\
&= [\cos\theta, \sin\theta (\frac{\sqrt 2}{2}\vec{i} + \frac{\sqrt 2}{2}\vec{k})]\\
\pmb{q}^{-1} &= [\cos\theta, -\sin\theta \hat{\vec{v}}]\\
&= [\cos\theta, -\sin\theta (\frac{\sqrt 2}{2}\vec{i} + \frac{\sqrt 2}{2}\vec{k})]\\
\end{aligned}
$$
Thus,
$$
\begin{aligned}
\pmb{qp} &= [-1, \sqrt 2 \vec{i} + \vec{j}]\\
\pmb{qpq^{-1}} &= [0, \vec{i} + \sqrt 2 \vec{j} + \vec{k}]
\end{aligned}
$$
Which is a pure quaternion and the norm of the result is:
$$
|\pmb{p’}| = 2
$$
but the vector has been rotated 90° rather than 45° which is twice as much as desired!
So in order to correctly rotate a vector $\vec{p}$ by an angle $\theta$ about an arbitrary axis $\widehat{\vec{v}}$ , we must consider the half-angle and construct the following quaternion:
$$
\pmb{q} = [\cos \frac{1}{2} \theta, \sin \frac{1}{2} \theta \widehat{\vec{v}}]
$$
Quaternion Interpolation
slerp: Spherical Linear interpolation. The slerp operation is useful because it allows us to smoothly interpolate between two orientations.
🌟Deduce Slerp
First, recall how we interpolation between scalar, the simple linear interpolation is:
$$
\begin{aligned}
&\Delta a = a_1 - a_0\\
&lerp(a_0, a_1, t) = a_0 + t\Delta a, t \in [0,1]
\end{aligned}
$$
Now we use the same basic idea in quaterninon:
- Compute the difference between the two values.
$$
\Delta q = q_1 q_0^{-1}
$$
- Take a fraction of this difference.
$$
(\Delta q)^t
$$
The meaning of quaternion exponentiation is similar to that of real numbers.
Recall that for any scalar $a$, besides zero, $a^0 = 1$ and $a^1 = a$. As the exponent $t$ varies from $0$ to $1$ the value of at varies from $1$ to $a$.
A similar statement holds for quaternion exponentiation: as $t$ varies from $0$ to $1$ the quaternion exponentiation $\pmb{q}^t$ varies from $[1, \pmb{0}]$ to $\pmb{q}$.
- Take the original value and adjust it by this fraction of the difference.
$$
(\Delta q)^tq_0
$$
Thus, the equation for slerp is given by:
$$
slerp(q_0, q_1, t) = (q_1 q_0^{-1})^tq_0, t \in [0,1]
$$
Hard to understand, right? Why there’s no adding operation? Don’t worry, next we give you the adding formula.
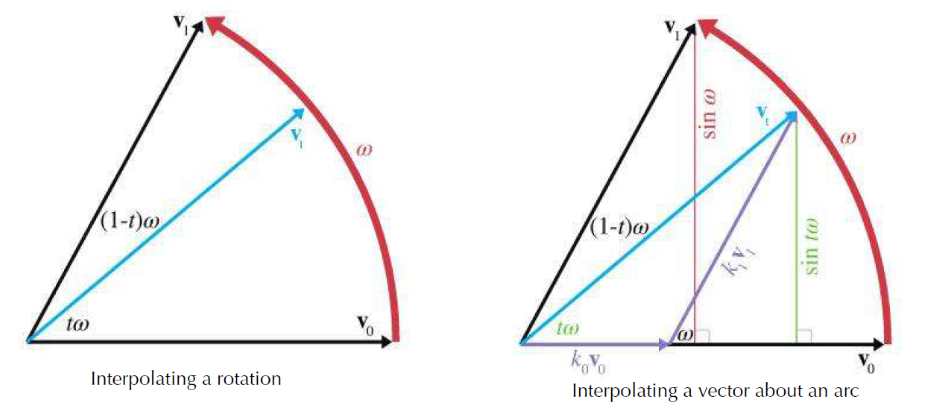
Imagine two 2D vectors $v_0$ and $v_1$, both of unit length. We wish to compute the value of $v_t$, which is the result of smoothly interpolating around the arc by a fraction $t$ of the distance from $v_0$ to $v_1$.
If we let $\omega$ be the angle intercepted by the arc from $v_0$ to $v_1$, then $v_t$ is the result of rotating $v_0$ around this arc by an angle of $t\omega$.
Let,
$$
v_t = k_0v_0 + k_1v_1
$$
相似三角形, we find,
$$
\sin \omega = \frac{\sin t\omega}{k_1} \longrightarrow
k_1 = \frac{\sin t\omega}{\sin \omega}
$$
similar,
$$
k_0 = \frac{\sin (1-t)\omega}{\sin \omega}
$$
thus,
$$
slerp(q_0, q_1, t) = \frac{\sin (1-t)\omega}{\sin \omega} q_0 + \frac{\sin t\omega}{\sin \omega} q_1
$$
We just need a way to compute $\omega$, the “angle” between the two quaternions.
Appendix
$$
OpenGL-perspective-matrix:
\begin{bmatrix}
\frac{1}{aspect _ ratio \cdot tan\frac{\theta}{2}} & 0 & 0 & 0 \\
0 & \frac{1}{tan \frac{\theta}{2}} & 0 & 0 \\
0 & 0 & \frac{zFar+zNear}{zNear-zFar}& \frac{2 \cdot zNear \cdot zFar}{zNear-zFar} \\
0 & 0 & -1 & 0 \\
\end{bmatrix} $$
$$
OpenGL-perspective-matrix:
\begin{bmatrix}
\frac{2|n|}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\
0 & \frac{2|n|}{t-b} & \frac{t+b}{t-b} & 0 \\
0 & 0 & \frac{|n|+|f|}{|n|-|f|} & \frac{2|f||n|}{|n|-|f|} \\
0 & 0 & -1 & 0 \\
\end{bmatrix} $$
$$
OpenGL-orthographic-matrix:
\begin{bmatrix}
\frac{1}{aspect _ ratio*tan \frac{\theta}{2}} & 0 & 0 & 0 \\
0 & \frac{1}{tan \frac{\theta}{2}} & 0 & 0 \\
0 & 0 & \frac{2}{zNear-zFar} & \frac{zNear+zFar}{zNear-zFar} \\
0 & 0 & 0 & 1 \\
\end{bmatrix} $$
so,for the OpenGL conventions, we can tell whether a projection matrix is perspective or orthographic based on the bottom row.
$$
OpenGL-Perspective
\begin{bmatrix} 0 & 0 & -1 & 0 \end{bmatrix}
$$
$$
penGL-Orthographic
\begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}
$$
$$
Dx-orthographic-matrix:
\begin{bmatrix}
\frac{2}{w} & 0 & 0 & 0 \\
0 & \frac{2}{h} & 0 & 0 \\
0 & 0 & \frac{1}{zF-zN} & 0 \\
0 & 0 & \frac{zn}{zN-zF} & 1 \\
\end{bmatrix}
$$
$$
Dx-perspective-matrix:
\begin{bmatrix}
\frac{1}{aspect _ ratio*tan \frac{\theta}{2}} & 0 & 0 & 0 \\
0 & \frac{1}{tan \frac{\theta}{2}} & 0 & 0 \\
0 & 0 & \frac{zF}{zF-zN} & 1 \\
0 & 0 & \frac{zN \cdot zF}{zN-zF} & 1 \\
\end{bmatrix}
$$
OpenGL use column vectors, Projection_Matrix * View_Matrix * Model_Matrix * Vector
Directx use row vectors, Vector * Model_Matrx * View_Matrx * Projection_Matrix

