Keywords: Polynomial, Binary, Floating, Matlab
This is the Chapter0 ReadingNotes from book Numerical Analysis by Timothy.
EVALUATING A POLYNOMIAL
What is the best way to evaluate
$$
P(x) = 2x^4 + 3x^3 -3x^2 + 5x - 1
$$
nested multiplication or Horner’s method:
$$
P(x) =−1 + x ∗ (5 + x ∗ (−3 + x ∗ (3 + x ∗ 2)))
\tag{0.2}
$$
evaluates the polynomial in $4$ multiplications and $4$ additions.
A general degree $d$ polynomial can be evaluated in $d$ multiplications and $d$ additions.
While the standard form for a polynomial $c_1 + c_2x + c_3x^2 + c_4x^3 + c_5x^4$ can be written in nested form as
$$
c_1 + x(c_2 + x(c_3 + x(c_4 + x(c_5))))
\tag{0.4}
$$
In particular, interpolation calculations in Chapter 3 will require the form
$$
c_1 + (x − r_1)(c_2 + (x − r_2)(c_3 + (x − r_3)(c_4 + (x − r_4)(c_5))))
\tag{0.5}
$$
where we call $r_1,r_2,r_3$, and $r_4$ the base points.
1 | %nest.m |
BINARY NUMBERS
$$
4 = (100.)_2, \frac{3}{4} = (0.11)_2
$$
Decimal to binary
$$
(53.7)_{10} = (53)_2 + (0.7)_2 = (?)_2
$$
Integer part
Convert decimal integers to binary by dividing by $2$ successively and recording the remainders.
$$
53 \div 2 = 26 … 1\\
26 \div 2 = 13 … 0\\
13 \div 2 = 6 … 1\\
6 \div 2 = 3 … 0\\
3 \div 2 = 1 … 1\\
1 \div 2 = 0 … 1\\
$$
$$
(53)_10 = (110101.)_2.
$$
Fractional part
Convert $(0.7)_10$ to binary by reversing the preceding steps. Multiply by $2$ successively and record the integer parts, moving away from the decimal point to the
right.
$$
.7 × 2 = .4 + 1\\
.4 × 2 = .8 + 0\\
.8 × 2 = .6 + 1\\
.6 × 2 = .2 + 1\\
.2 × 2 = .4 + 0\\
.4 × 2 = .8 + 0\\
\cdots
$$
$$
(0.7)_10 = (.1011001100110. . .)_2 = (.1\overline{0110})_2,
$$
Thus,
$$
(53.7)_{10} = (53)_2 + (0.7)_2 = (110101.1\overline{0110})2.
$$
Binary to decimal
Integer part
$$
(10101)_2 = 1 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0
= (21)_{10}
$$
Fractional part
$$
(.1011)_2 = \frac{1}{2} + \frac{1}{8} + \frac{1}{16}= (\frac{11}{16})_{10}
$$
What if the fractional part is not a finite base 2 expansion?
💡For example💡:
$$
x = (0.\overline{1011})_2
$$
Solution:
Multiply $x$ by $2^4$, which shifts $4$ places to the left in binary.
$$
2^4x = (1011.\overline{1011})_2
$$
Thus,
$$
(2^4-1)x = (1011)_2 = (11)_{10}
$$
So that
$$
x = \frac{11}{15}
$$
What if the fractional part does not immediately repeat?
💡For example💡:
$$
x = (0.10\overline{101})_2
$$
Solution:
Multiplying by $2^2$ shifts to $y = 2^2x = 10.\overline{101}$. The fractional part of $y$, call it $z = .\overline{101}$, is calculated as before:
$$
2^3z = 101.\overline{101}\\
z = 000.\overline{101}
$$
Therefore,
$$
7z = 5
$$
$$
y = 2 + \frac{5}{7}
$$
$$
x = 2^{-2}y = \frac{19}{28}
$$
FLOATING POINT REPRESENTATION OF REAL NUMBERS
Simple algorithms, such as Gaussian elimination or methods for solving differential equations, can magnify microscopic errors to macroscopic size.
Floating point formats
The IEEE standard consists of a set of binary representations of real numbers. A floating point number consists of three parts: the sign (+ or −)(符号位), a mantissa(尾数), which contains the string of significant bits, and an exponent(指数). The three parts are stored together in a single computer word(字).
word, Byte, bit
1Byte = 8bit
computer word: 16,32,64 bits
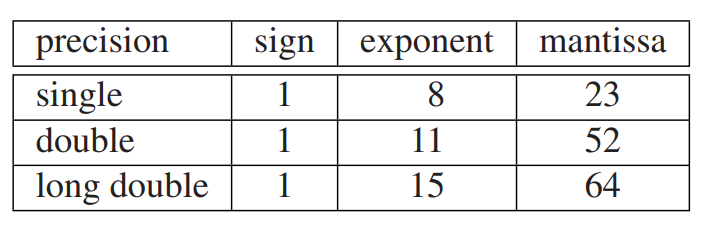
The form of a normalized IEEE floating point number is
$$
\pm 1.bbb \cdots b \times 2^p
\tag{0.6}
$$
where each of theN $b$’s is $0$ or $1$, and $p$ is an $M$-bit binary number representing the exponent.
The double precision number $1$ is
$$
+1. \underbrace{0000000000000000000000000000000000000000000000000000}_{52} × 2^0
$$
where we have 52 bits of the mantissa. The next floating point number greater than $1$ is
$$
+1. \underbrace{0000000000000000000000000000000000000000000000000001}_{52} × 2^0
$$
which is $1 + 2^{−52}$.
DEFINITION 0.1
The number machine epsilon, denoted $\epsilon_{match}$, is the distance between $1$ and the smallest floating point number greater than $1$.
For the IEEE double precision floating point standard,
$$
\epsilon_{match} = 2^{-52}
$$
How do we fit the infinite binary number representing 9.4 in a finite number of bits?
IEEE Rounding to Nearest Rule
For double precision, if the 53rd bit to the right of the binary point is 0, then round down (truncate after the 52nd bit). If the 53rd bit is 1, then round up (add 1 to the 52 bit), unless all known bits to the right of the 1 are 0’s, in which case 1 is added to bit 52 if and only if bit 52 is 1.
$$
9.4 = +1. \underbrace{0010110011001100110011001100110011001100110011001100}_{52} 110 \cdots × 2^3
$$
$$
fl(9.4) = +1. \underbrace{0010110011001100110011001100110011001100110011001101}_{52} × 2^3
$$
DEFINITION 0.2
Denote the IEEE double precision floating point number associated to $x$, using the Rounding to Nearest Rule, by $fl(x)$.
Obviously, for 9.4, we discarding the infinite tail
$$
\begin{aligned}
.\overline{1100} \times 2^{-52} \times 2^3
&=.\overline{0110} \times 2^{-51} \times 2^3 \\
&= .4 \times 2^{-48}
\end{aligned}
$$
from the right end of the number.
Then, we adding $2^{-52} \times 2^3 = 2^{-49}$ in the rounding step.
Therefore,
$$
\begin{aligned}
fl(9.4) &= 9.4 + 2^{-49} - .4 \times 2^{-48} \\
&= 9.4 + 0.2 \times 2^{-49}
\end{aligned}
\tag{0.8}
$$
We call $0.2 \times 2^{-49}$ the rounding error.
DEFINITION 0.3
Let $x_c$ be a computed version of the exact quantity $x$. Then
$$
absolute-error = |x_c - x|
$$
and
$$
relative-error = \frac{|x_c - x|}{x}
$$
Relative rounding error
In the IEEE machine arithmetic model, the relative rounding error of $fl(x)$ is no more than one-half machine epsilon:
$$
\frac{|fl(x) - x|}{x} \leq \frac{1}{2} \epsilon_{match}
$$
Machine representation
Each double precision floating point number is assigned an $8$-byte word, or $64$ bits, to store its three parts. Each such word has the form
$$
se_1e_2 . . . e_{11}b_1b_2 . . . b_{52}
\tag{0.10}
$$
11 bits representing the exponent and 52 bits following the decimal point, representing the mantissa.
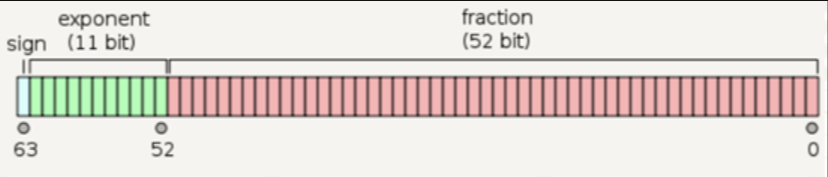
$11$ bits can represent $2^{11} = 2048$ states $\longrightarrow [0,2047]$.
In left-justifying, we find that the exponent can be negative, like $0.4 = 1.10\overline{0110} \times 2^{-2}$.
For brevity, we don’t want to consider negative in computer exponents. So we introduce a exponent bias.
In double precision, the exponent bias is $2^{10}-1 = 1023$.
So that, for left-justifying double exponent $[-1022, 1023]$, the computer exponent covers $[1, 2046]$.
💡For example💡:
$$
1 = +1. \underbrace{0000000000000000000000000000000000000000000000000000}_{52} × 2^0,
$$
Adding the exponent bias to $0$, we get $1023$, so the double precision machine number form is
$$
\boxed{0}\boxed{01111111111}\boxed{0000000000000000000000000000000000000000000000000000}
$$
the hex format is
$$
3FF0000000000000
$$
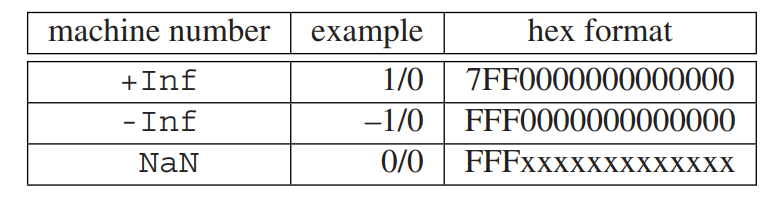
What about 0 and 2017 ? >>>> $0$ and $2047$ for special purposes.
$2047$, is used to represent $\infty$ if the mantissa bit string is all zeros and NaN, which stands for Not a Number,otherwise.
the first twelve bits of Inf and -Inf are $\boxed{0111} \boxed{1111} \boxed{1111}$ and $\boxed{1111} \boxed{1111} \boxed{1111}$ , respectively, and the remaining 52 bits (the mantissa) are zero. The machine number NaN also begins$\boxed{1111} \boxed{1111} \boxed{1111}$ but has a nonzero mantissa.
The special exponent 0, also denotes a departure from the standard floating point form. In this case the machine number is interpreted as the non-normalized floating point number
$$
\pm 0.\boxed{b_1b_2\cdots b_{52}} \times 2^{-1022}
\tag{0.11}
$$
These non-normalized numbers are called subnormal floating point numbers. They extend the range of very small numbers by a few more orders of magnitude.
Therefore, $2^{−52} × 2^{−1022} = 2^{−1074}$ is the smallest nonzero representable number in double precision. Its machine word is
$$
\boxed{0} \boxed{00000000000} \boxed{0000000000000000000000000000000000000000000000000001}
$$
The subnormal numbers include the most important number $0$.
Addition of floating point numbers
💡For example💡:
Calculate $9.4-9-0.4$ in Computer.
Solution:
9.4 is stored as
$$
9.4 + 0.2 \times 2^{-49}
$$
thus,
$$
9.4 - 9 = 0.4 + 0.2 \times 2^{-49}
$$
Since, 0.4 is stored as
$$
fl(0.4) = 0.4 + 0.1 \times 2^{-52}
$$
so, the result is
$$
0.2 \times 2^{-49} - 0.1 \times 2^{-52} = 3 \times 2^{-53}
$$
1 | >> format long |
LOSS OF SIGNIFICANCE(丢失有效数字)
💡For example💡:
We assume that we are using a three-decimal-digit computer. Now Calculate $\sqrt{9.01} - 3$.
Solution:
Checking on a hand calculator, we see that the correct answer is approximately $0.0016662 = 1.6662 × 10^{−3}$.
But in Computer, $\sqrt{9.01} \approx 3.0016662$, we store it as $3.00$. Subtracting $3.00$, we get a final answer of $0.00$.
No significant digits in our answer are correct.
What is causing the loss of significance is the fact that we are explicitly subtracting nearly equal numbers, We can avoid this problem by using algebra to rewrite the expression:
$$
\sqrt{9.01} - 3 = \frac{(\sqrt{9.01} - 3) (\sqrt{9.01} + 3)}{\sqrt{9.01} + 3}
\approx 1.67 \times 10^{-3}
$$
The lesson is that it is important to find ways to avoid subtracting nearly equal numbers in calculations, if possible.
Often, specific identities can be used, as with trigonometric expressions.
💡For example💡:
Compare the two expressions:
$$
E_1 = \frac{1-\cos x}{\sin ^2 x}, E_2 = \frac{1}{1+\cos x}
$$
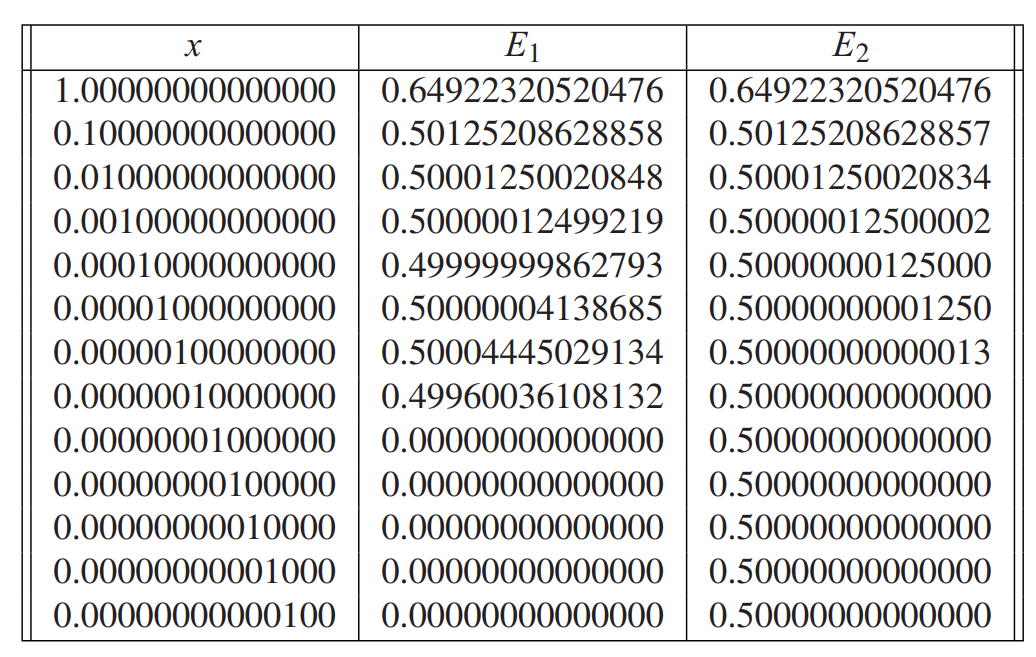
$E_2$ is better than $E_1$.
The quadratic formula is often subject to loss of significanc

