Keywords: Bisection Method, Fixed-point Method, Newton’s Method, Brent’s Method, Kinematics, Matlab
This is the Chapter1 ReadingNotes from book Numerical Analysis by Timothy.
THE BISECTION METHOD
Bracketing a root(二分法)
DEFINITION 1.1
The function $f(x)$ has a root at $x = r$ if $f(r) = 0$.
This fact is summarized in the following corollary of the 👉Intermediate Value Theorem:
THEOREM 1.2
Let $f$ be a continuous function on $[a,b]$, satisfying $f(a)f(b) < 0$. Then $f$ has a root between $a$ and $b$, that is, there exists a number $r$ satisfying $a < r < b$ and $f (r) = 0$.
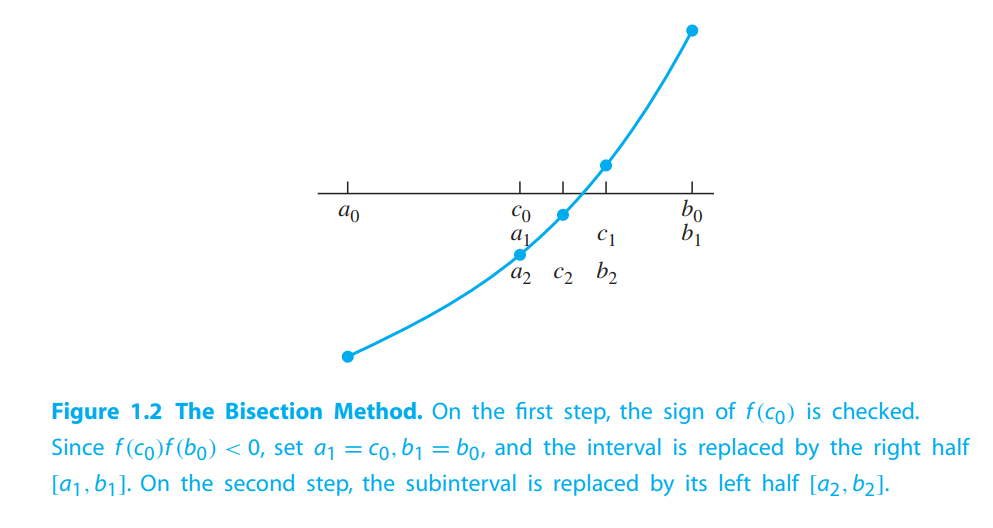

The algorithm can be written in the following Matlab code:
1 | %bisect.m |
How accurate and how fast?
If $[a,b]$ is the starting interval, then after $n$ bisection steps, the interval $[a_n,b_n]$ has length $(b − a)/2^n$.
Choosing the midpoint $x_c = (a_n + b_n)/2$ gives a best estimate of the solution $r$, which is within half the interval length of the true solution.
$$
\begin{aligned}
Solution-error &= |x_c - r| \\
&= |\frac{a_n + b_n}{2} - r| \\
&< \frac{b_n - a_n}{2} \\
&= \frac{b-a}{2^{n+1}}
\end{aligned}
\tag{1.1}
$$
and
$$
Function-evaluations = n + 2
\tag{1.2}
$$
DEFINITION 1.3
A solution is correct within $p$ decimal places if the error is less than $0.5 × 10^{−p}$ (在小数点后p位内正确).
💡For example💡:
Use the Bisection Method to find a root of $f(x) = cosx − x$ in the interval $[0,1]$ to within six correct places.
Solution:
$$
\frac{b-a}{2^{n+1}} < 0.5 \times 10^{-6}
$$
$$
n > 19.9
$$
Therefore, $n = 20$ steps will be needed.
FIXED-POINT ITERATION (FPI)
Fixed points of a function
DEFINITION 1.4
The real number $r$ is a fixed point of the function $g$ if $g(r) = r$.
The number $r = 0.7390851332$ is an approximate fixed point for the function $g(x) = cosx$. The function $g(x) = x^3$ has three fixed points, $r =−1, 0$, and $1$.

According to
(Continuous Limits) Let $f$ be a continuous function in a neighborhood of $x_0$, and assume $\lim_{n\rightarrow \infty}x_n = x_0$. Then
$$
\lim_{n \rightarrow \infty} f(x_n) = f(\lim_{n\rightarrow \infty} x_n) = f(x_0)
$$
we can get
$$
g(r) = g(\lim_{i\rightarrow \infty}x_i) = \lim_{i\rightarrow \infty} g(x_i) = r
$$
The Fixed-Point Iteration algorithm applied to a function g is easily written in Matlab code:
1 | %fpi.m |
Can every equation $f(x) = 0$ be turned into a fixed-point problem $g(x) = x$? Yes.
💡For example💡:
$$
x^3 + x - 1 = 0
\tag{1.4}
$$
Three Solutions: Initial value $x_0 = 0.5$
1.
$$
x = 1-x^3\longrightarrow g(x) = 1 - x^3
\tag{1.5}
$$
Instead of converging, the iteration tends to alternate between the numbers $0$ and $1$.
2.
$$
x = \sqrt[3]{1-x}\longrightarrow g(x) = \sqrt[3]{1-x}
\tag{1.6}
$$
This time FPI is successful.
3.
$$
3x^3 + x = 1 + 2x^3\\
x = \frac{1+2x^3}{1+3x^2}\longrightarrow g(x) = \frac{1+2x^3}{1+3x^2}
\tag{1.7}
$$
This time FPI is successful, but in a much more striking way.
Geometry of Fixed-Point Iteration
This geometric illustration of a Fixed-Point Iteration is called a cobweb diagram(蛛网图).
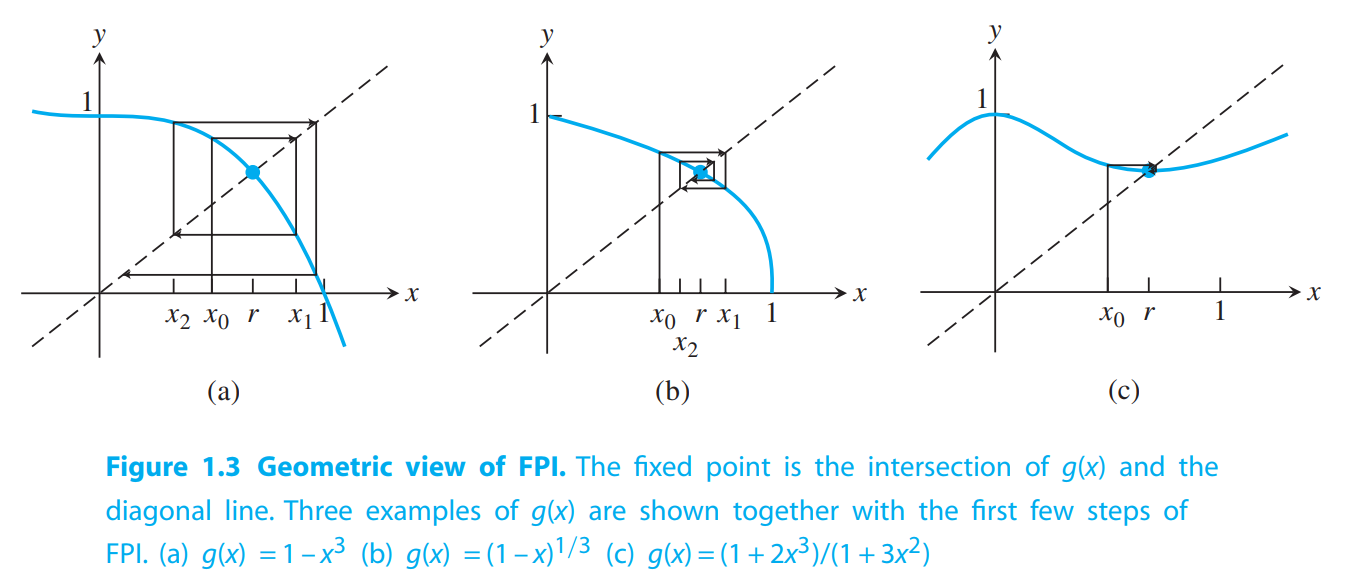
Linear convergence of Fixed-Point Iteration
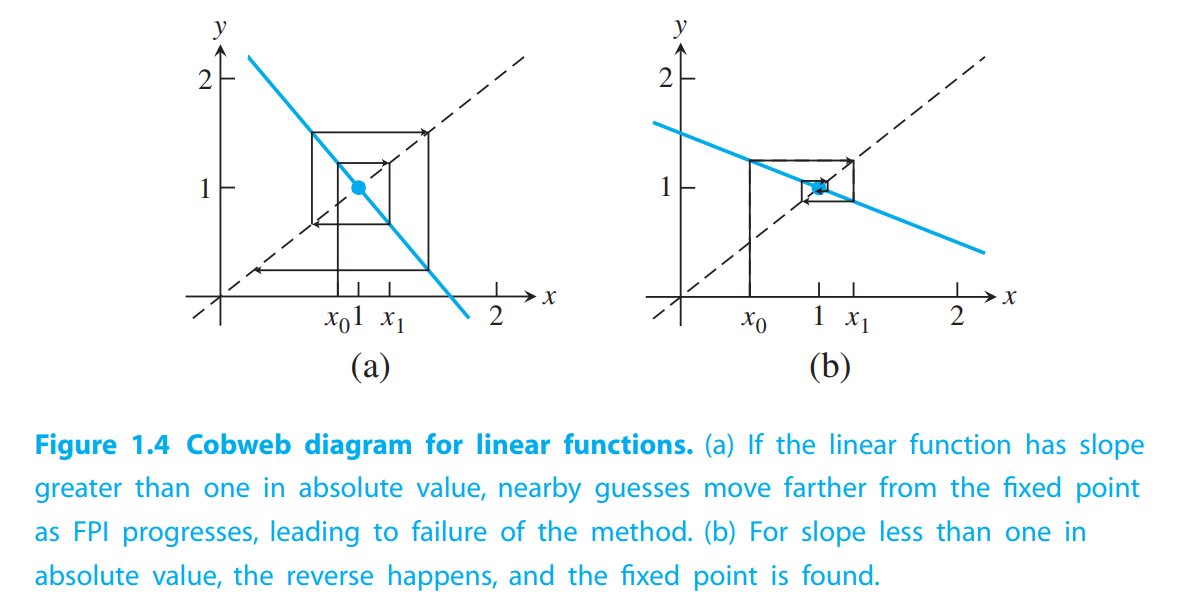
Figure1.4 shows Fixed-Point Iteration for two linear functions
$$
g_1(x) = -\frac{3}{2}x + \frac{5}{2}\\
g_2(x) = -\frac{1}{2}x + \frac{3}{2}
$$
From geometric view,
For $g_1(x)$, Because the slope of $g_1(x)$ at the fixed point is greater than one, the vertical segments(看箭头段), the ones that represent the change from $x_n$ to $x_{n+1}$, are increasing in length as FPI proceeds. As a result, the iteration “spirals out’’ from the fixed point $x = 1$, even if the initial guess $x_0$ was quite near.
For $g_2(x)$, it “spirals in”.
From equation view,
$$
g_1(x) = -\frac{3}{2}(x-1) + 1
$$
$$
g_1(x) - 1 = -\frac{3}{2}(x-1)
$$
$$
x_{i+1} - 1 = -\frac{3}{2}(x_i-1)
\tag{1.8}
$$
If we view $e_i = |r − x_i|$ as the error at step $i$ (meaning the distance from the best guess at step $n$ to the fixed point), we see from (1.8) that $e_{i+1} = \frac{3e_i}{2}$, implying that errors increase at each step by a factor of approximately $3/2$. This is divergence.
$g_2(x)$ is convergence.
DEFINITION 1.5
Let $e_i$ denote the error at step $i$ of an iterative method. If
$$
\lim_{i\rightarrow \infty} \frac{e_{i + 1}}{e_i} = S < 1
$$
the method is said to obey linear convergence with rate $S$.
THEOREM 1.6
Assume that $g$ is continuously differentiable, that $g(r) = r$, and that $S = |g’(r)| < 1$. Then Fixed-Point Iteration converges linearly with rate $S$ to the fixed point $r$ for initial guesses sufficiently close to $r$.
DEFINITION 1.7
An iterative method is called locally convergent to $r$ if the method converges to $r$ for initial guesses sufficiently close to $r$.
💡For example💡:
Calculate $\sqrt{2}$ by using FPI.
Solution:
Suppose we want to find the first $10$ digits of $\sqrt 2$. Start with the initial guess $x_0 = 1$.
Obviously this guess is too low, we want to find a fomula to change 1 to higher number to approximate $\sqrt{2}$.
Obviously $\frac{2}{1}$ seems too high.
In fact, any initial guess $0 < x_0 < 2$, together with $\frac{2}{x_0}$, form a bracket for $\sqrt{2}$. (像一对括号一样,不断逼近$\sqrt{2}$)
We guess
$$
x_1 = \frac{1 + \frac{2}{1}}{2} = \frac{3}{2}
$$
$$
x_2 = \frac{\frac{3}{2} + \frac{4}{3}}{2} = 1.4\overline{16}
$$
$$
x_3 = \frac{\frac{17}{12} + \frac{24}{17}}{2} \approx 1.414215686
$$
The FPI we are executing is
$$
x_{i+1} = \frac{x_i + \frac{2}{x_i}}{2}
$$
Note that $\sqrt{2}$ is a fixed point of the iteration.
$$
g’(\sqrt{2}) = 0
$$
Stopping criteria
an absolute error stopping criterion
$$
|x_{i+1} - x_{i}| < TOL
\tag{1.16}
$$
the relative error stopping criterion
$$
\frac{|x_{i+1} - x_{i}|}{|x_{i+1}|} < TOL
\tag{1.17}
$$
A hybrid absolute/relative stopping criterion such as
$$
\frac{|x_{i+1} - x_{i}|}{max(|x_{i+1}|, \theta)} < TOL
\tag{1.18}
$$
LIMITS OF ACCURACY
Working in double precision means that we store and operate on numbers that are kept to 52-bit accuracy, about 16 decimal digits.
Forward and backward error
💡For example💡:
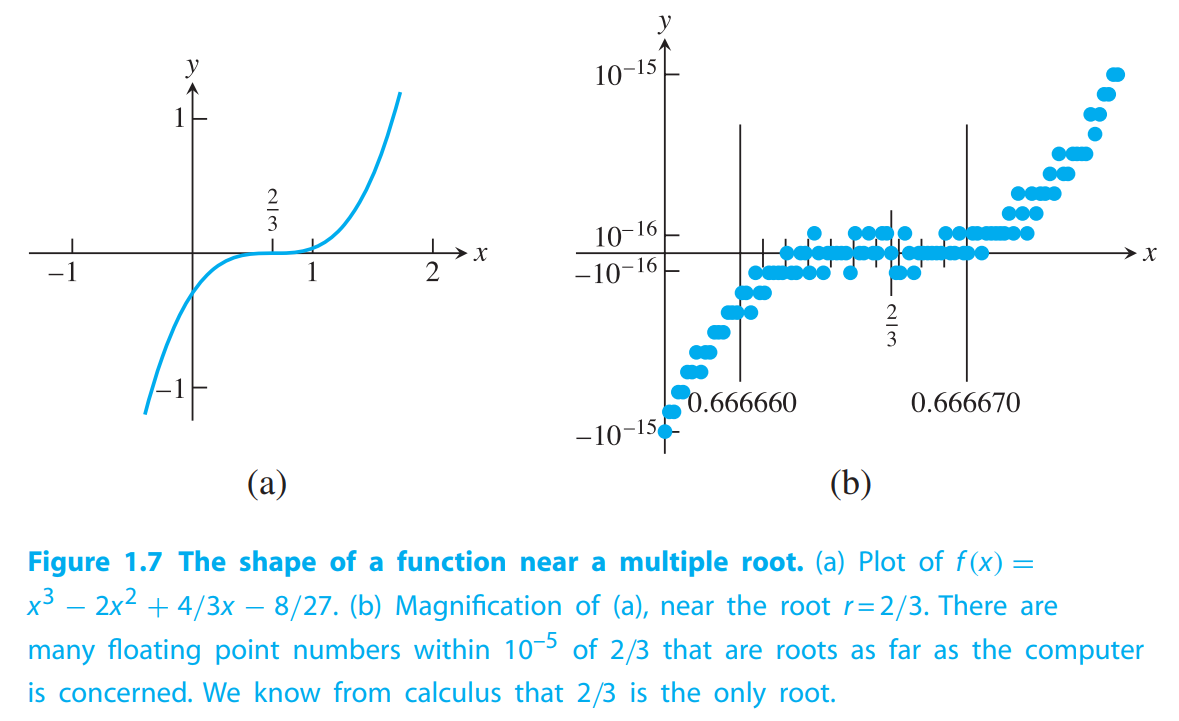
Use the Bisection Method to find the root of $f (x) = x^3 − 2x^2 + \frac{4}{3}x − \frac{8}{27}$ to within six correct significant digits(6个正确的有效位).
Solution:
$20$ bisection steps should be sufficient for six correct places.
In fact, it is easy to check without a computer that $r = 2/3 = 0.666666666. . .$ is a root:
How many of these digits can the Bisection Method obtain?
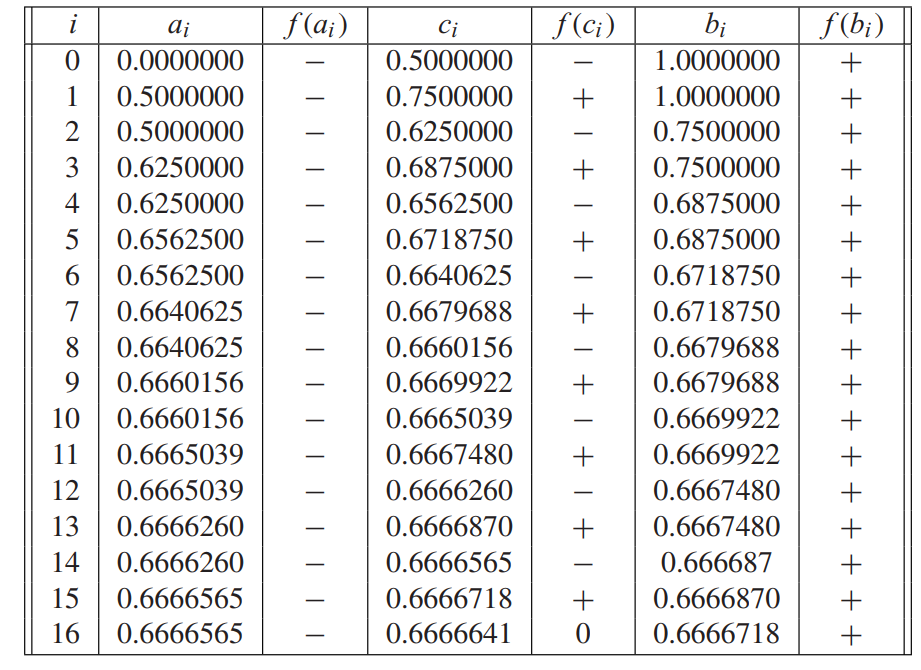
From the figure above, we can see that Bisection Method stops after 16 steps, because the computer get $f(0.6666641) = 0$, satisfying the stop condition.
From Figure1.7, we can see that the computer thinks there are many floating point numbers within $10^{−5}$ of the correct root $r = 2/3$ that are evaluated to machine zero, and therefore have an equal right to be called the root!
This is not the method fault, but the computer! (Computer is not precise enough!) If the computer arithmetic is showing the function to be zero at a nonroot, there is no way the method can recover.
DEFINITION 1.8
Assume that $f$ is a function and that $r$ is a root, meaning that it satisfies $f(r) = 0$. Assume that $x_a$ is an approximation to $r$. For the root-finding problem, the backward error of the approximation $x_a$ is $|0 - f(x_a)|$ and the forward error is $|r − x_a|$.
Backward error is on the left or input (problem data) side. It is the amount we would need to change the problem (the function $f$ ) to make the equation balance with the output approximation $x_a$, which is $|0-f(x_a)|$.
Forward error is the error on the right or output (problem solution) side. It is the amount we would need to change the approximate solution to make it correct, which is $|r - x_a|$.
The difficulty with Example 1.7 is that, according to Figure 1.7, the backward error is near $\epsilon_{mach} \approx 2.2 \times 10^{−16}$, while forward error is approximately $10^{−5}$. Double precision numbers cannot be computed reliably below a relative error of machine epsilon($2^{-52}$ for double precision).
Since the backward error cannot be decreased further with reliability, neither can the forward error.
(总结来讲,到了第16步,计算的数值已经超出double的精度了,所以不会再迭代精确了…)
DEFINITION 1.9
Assume that $r$ is a root of the differentiable function $f$; that is, assume that $f(r) = 0$. Then if $0 = f(r) = f’(r) = f’’(r) = \cdots = f^(m−1)(r)$, but $f^{(m)}(r) \neq 0$, we say that $f$ has a root of multiplicity $m$ at $r$. We say that $f$ has a multiple root at $r$ if the multiplicity is greater than one. The root is called simple if the multiplicity is one.
For example, $f(x) = x^2$ has a multiplicity two, or double, root at $r = 0$, because $f(0) = 0,f’(0) = 2(0) = 0$, but $f’’(0) = 2 \neq 0$.
Back to Figure1.7, Because the graph of the function is relatively flat near a multiple root, a great disparity exists between backward and forward errors for nearby approximate solutions. The backward error, measured in the vertical direction, is often much smaller than the forward error, measured in the horizontal direction.
TheWilkinson polynomial
The Wilkinson polynomial is
$$
W(x) = (x − 1)(x − 2) · · · (x − 20)
\tag{1.19}
$$
which, when multiplied out, is
$$
\begin{aligned}
W(x) = &x^{20} − 210x^{19} + 20615x^{18} − 1256850x^{17} + 53327946x^{16} − 1672280820x^{15}\\
&+ 40171771630x^{14} − 756111184500x^{13} + 11310276995381x^{12}\\
&− 135585182899530x^{11} + 1307535010540395x^{10} − 10142299865511450x^{9}\\
&+ 63030812099294896x^{8} − 311333643161390640x^{7}\\
&+ 1206647803780373360x^{6} − 3599979517947607200x^{5}\\
&+ 8037811822645051776x^{4}− 12870931245150988800x^{3}\\
&+ 13803759753640704000x^{2} − 8752948036761600000x\\
&+ 2432902008176640000
\end{aligned}
\tag{1.20}
$$
The roots are the integers from $1$ to $20$. However, when $W(x)$ is defined according to its unfactored(没有因式分解的形式) form (1.20), its evaluation suffers from cancellation of nearly equal, large numbers.
Sensitivity of root-finding
Small floating point errors in the equation can translate into large errors in the root. To understand what causes this magnification of error, we will establish a formula predicting how far a root moves when the equation is changed.
Assume that the problem is to find a root $r$ of $f(x) = 0$, but that a small change $\epsilon g(x)$ is made to the input, where $\epsilon$ is small. Let $\Delta r$ be the corresponding change in the root, so that
$$
f(r+\Delta r) + \epsilon g(r + \Delta r) = 0
$$
Expanding $f$ and $g$ in 👉degree-one Taylor polynomials >> implies that
$$
f(r) + (\Delta r) f’(r) + \epsilon g(r) + \epsilon(\Delta r)g’(r) + O((\Delta r)^2) = 0
$$
For small $\Delta r$, the $O((\Delta r)^2)$ terms can be neglected to get
$$
(\Delta r) (f’(r) + \epsilon g’(r)) \approx -f(r)-\epsilon g(r) = -\epsilon g(r)
$$
or
$$
\Delta r \approx \frac{-\epsilon g(r)}{f’(r)+\epsilon g’(r)} \approx -\epsilon \frac{g(r)}{f’(r)}
$$
assuming that $\epsilon$ is small compared with $f’(r)$, and in particular, $f’(r) \neq 0$.
Sensitivity Formula for Roots
Assume that $r$ is a root of f(x) and $r + \Delta r$ is a root of $f(x) + \epsilon g(x)$. Then,
$$
\Delta r \approx -\epsilon \frac{g(r)}{f’(r)}
$$
if $\epsilon \ll f’(r)$
A problem with high condition number is called ill-conditioned, and a problem with a condition number near $1$ is called well-conditioned.
NEWTON’S METHOD
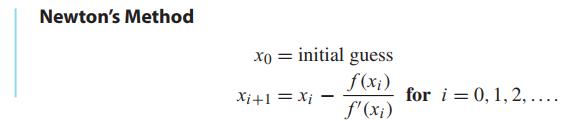
Quadratic convergence of Newton’s Method
DEFINITION 1.10
Let $e_i$ denote the error after step $i$ of an iterative method. The iteration is quadratically convergent(成平方收敛) if
$$
M = \lim_{i\rightarrow \infty} \frac{e_{i+1}}{e_i^2} < \infty
$$
THEOREM 1.11
Let $f$ be twice continuously differentiable and $f(r) = 0$. If $f’(r) \neq 0$, then Newton’s Method is locally and quadratically convergent to $r$. The error $e_i$ at step $i$ satisfies
$$
\lim_{i \rightarrow \infty} \frac{e_{i+1}}{e_i^2} = M
$$
where
$$
M = \frac{f’’(r)}{2f’(r)}
$$
Linear convergence of Newton’s Method
THEOREM 1.12
Assume that the $(m + 1)$-times continuously differentiable function $f$ on $[a,b]$ has a multiplicity $m$ root at $r$. Then Newton’s Method is locally convergent to $r$, and the error $e_i$ at step $i$ satisfies
$$
\lim_{i \rightarrow \infty} \frac{e_{i+1}}{e_i} = S
\tag{1.29}
$$
where,
$$
S = (m-1)/m,
$$
If the multiplicity of a root is known in advance, convergence of Newton’s Method can be improved with a small modification.
THEOREM 1.13
If f is $(m + 1)$-times continuously differentiable on $[a,b]$, which contains a root $r$ of multiplicity $m>1$, then Modified Newton’s Method
$$
x_{i+1} = x_i - \frac{mf(x_i)}{f’(x_i)}
\tag{1.32}
$$
converges locally and quadratically to $r$.
💡For example💡:
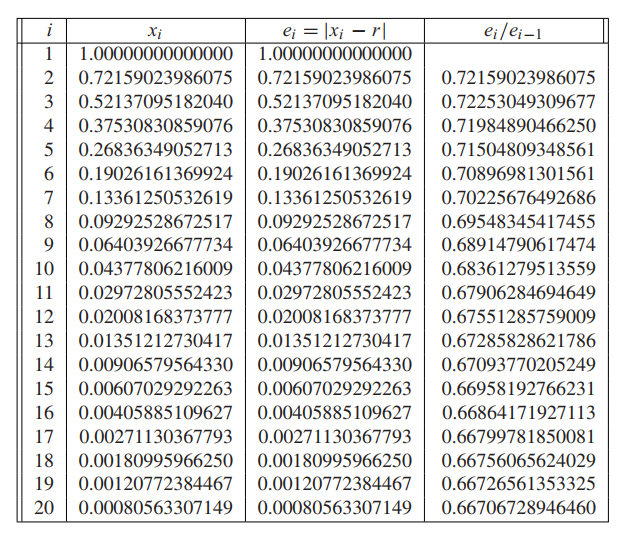
Find the multiplicity of the root $r = 0$ of $f(x) = \sin x + x^2 \cos x − x^2 − x$, and estimate the number of steps of Newton’s Method required to converge within six correct places (use $x_0 = 1$).
Solution:
$$
f(x) = \sin x + x^2 \cos x - x^2 - x\\
f’(x) = \cos x + 2x \cos x - x^2 \sin x - 2x - 1\\
f’’(x) = -\sin x + 2 \cos x - 4x\sin x - x^2 \cos x - 2\\
$$
and that each evaluates to $0$ at $r = 0$. The third derivative,
$$
f’’’(x) = -\cos x - 6\sin x - 6x \cos x + x^2 \sin x
\tag{1.30}
$$
satisfies $f(0)=−1$, so the root $r = 0$ is a triple root, meaning that the multiplicity is $m = 3$. By Theorem 1.12, Newton should converge linearly with $e_{i+1} \approx \frac{2e_i}{3}$.
So that
$$
(\frac{2}{3})^n < 0.5 \times 10^{-6}\\
n > 35.78
$$
Approximately 36 steps will be needed. The first 20 steps are shown in the table.
But if we apply Modified Newton’s Method to achieve quadratic convergence. After five steps, convergence to the root $r = 0$ has taken place to about eight digits of accuracy:
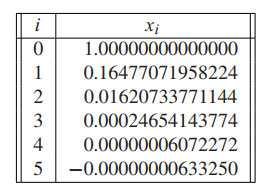
ROOT-FINDING WITHOUT DERIVATIVES
Brent’s Method, a hybrid method which combines the best features of iterative and bracketing methods.
Secant Method and variants
The Secant Method is similar to the Newton’s Method, but replaces the derivative by a difference quotient.
An approximation for the derivative at the current guess $x_i$ is the difference quotient
$$
\frac{f(x_i) - f(x_{i-1})}{x_i - x_{i-1}}
$$
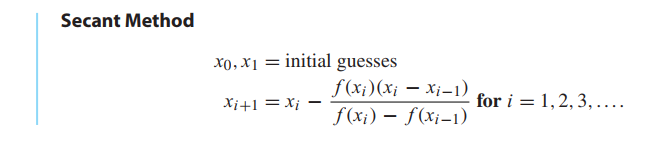
Unlike Fixed-Point Iteration and Newton’s Method, two starting guesses are needed to begin the Secant Method.
the approximate error relationship of Secant Method is
$$
e_{i+1} \approx |\frac{f’’(r)}{2f’(r)}| e_ie_{i-1}
$$
and it implies that
$$
e_{i+1} \approx |\frac{f’’(r)}{2f’(r)}|^{\alpha - 1}e_i^\alpha
$$
where $\alpha = (1 + \sqrt{5}) / 2 \approx 1.62$
The convergence of the Secant Method to simple roots is called superlinear, meaning that it lies between linearly and quadratically convergent methods.


